Final Assignment
Write-up by
Blair T. Dietrich
EMAT 6680
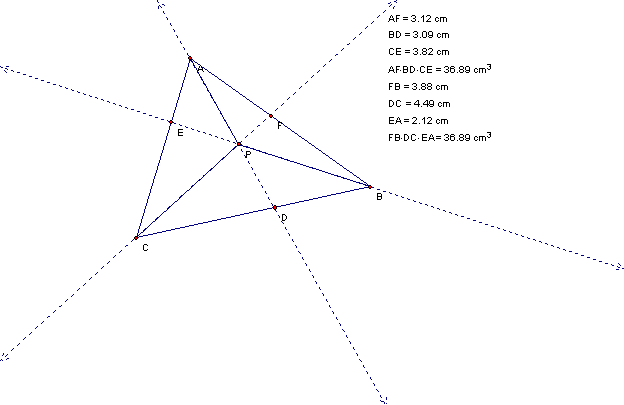
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
After exploring the products AF*BD*CE and FB*DC*EA by
manipulating triangle ABC and point P, I conjecture that AF*BD*CE = FB*DC*EA
or, equivalently, that ![]() .
.
One screen shot is shown below. Click here to try your own manipulations. This GSP file also allows P to be outside the triangle (and points D, E, and F to be on the lines containing segments BC, CA, and AB, respectively).
Proof:
Construct lines GH, IJ, and KL through point P parallel to lines AB, CA, and BC, respectively.
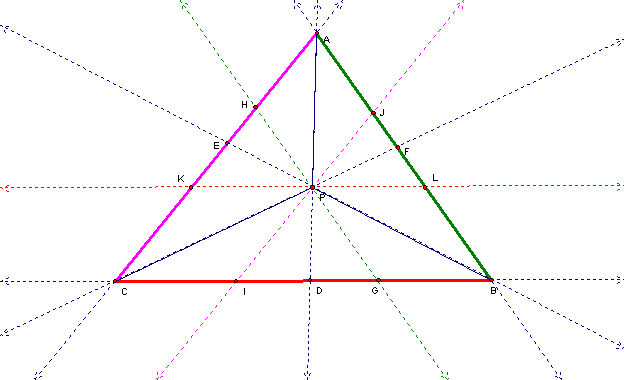
ΔAFC~ΔHPC by corresponding angles and the reflexive property. Similarly, ΔBFC~ΔGPC.
From these triangles we have the following:
AF/HP=FC/PC and BF/GP=FC/PC. By substitution, AF/HP=BF/GP or, equivalently, AF/BF=HP/GP.
ΔABE~ΔHPE and ΔABD~ΔPGD also by corresponding angles and the reflexive property.
From these triangles we have the following:
HP/AB=PE/BE and PG/AB=PD/AD. By division, HP/PG=(PE/BE)/(PD/AD).
Combining the results from the above two steps we have AF/BF=(PE/BE)/(PD/AD).
In a similar manner, it can be shown that ΔBDA~ΔLPA, ΔCDA~ΔKPA, ΔBCF~ΔLPF, ΔCBE~ΔKPE, and that BD/CD=(PF/CF)/(PC/BE).
Also in a similar manner, it can be shown that ΔCEB~ΔIPB, ΔAEB~ΔJPB, ΔCAD~ΔIPD, ΔACF~ΔJPF, and that CE/AE=(PD/AD)/(PF/CF).
We now can multiply these three statements together to obtain the following:
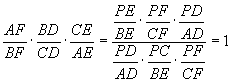
Further investigation:
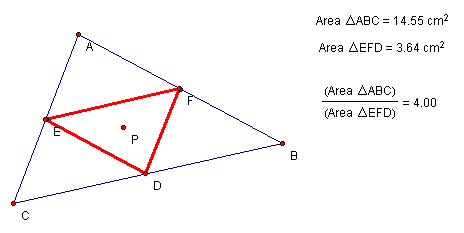
When P is inside triangle ABC, the ratio of areas of triangle ABC and triangle DEF is always greater than or equal to 4.
Here is one example:
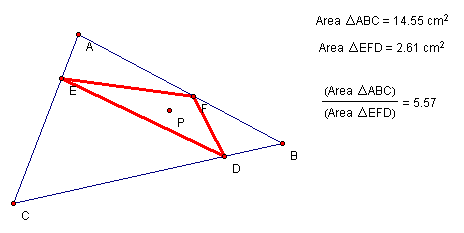
Try exploring on your own with this GSP sketch.
The ratio of areas will be equal to 4 when points D, E, and F are the midpoints of the sides of triangle ABC.