Assignment 11: The N Leaf Rose
By: David Drew
EMAT 6680, J. Wilson
In this investigation we want
to go through several explorations with what is known as the N Leaf Rose. What is
the N Leaf Rose and how does a rose relate to math? It is just an equation that
looks like a flower when you graph it for several different values. The
equations we want to look at and compare and contrast are 
first
and always in blue and 
second and always in red with different values
of k. The theta in our equation will range from 0 to 2pi.
We start with the most basic
of our equations with a = b = 1 and k = 0.
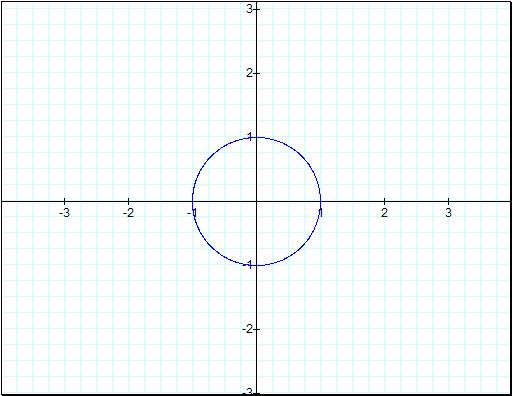
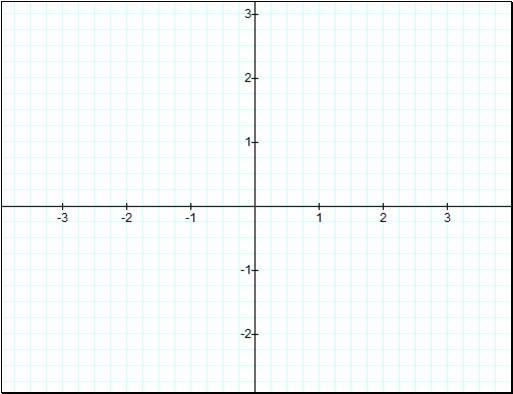
We notice that our second
equation doesn’t even appear in the graph. That’s because sin(0) = 0 so
therefore there is nothing at all. In the other case we have a 1 so it’s no
surprise that our first graph should have radius of 1. Let’s take it up a notch
and see what happens if k = 1.
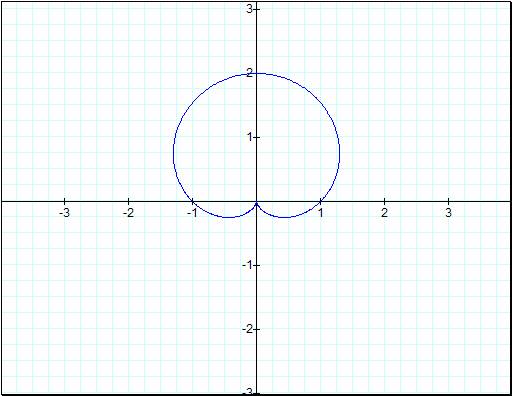
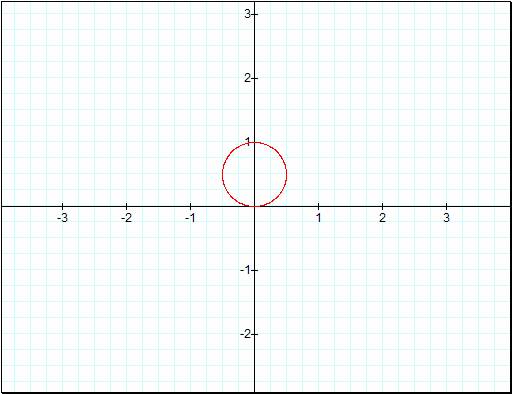
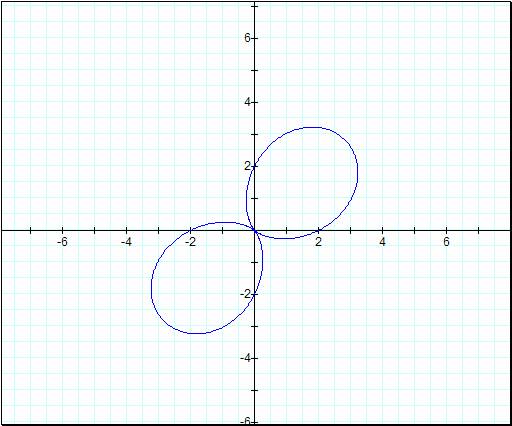
Now we start to see something
interesting in the first graph and our second graph have caught up a little by
just being visible. The image in graph one is obviously bigger than the second
one, and its shape is that of a cardioid while the shape in the second graph is
a lowly circle. Let’s continue to increase the value of k by one.
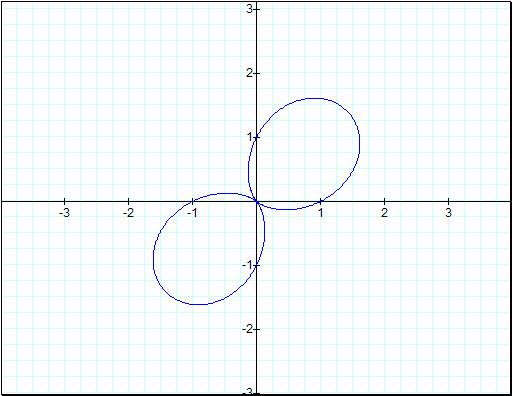
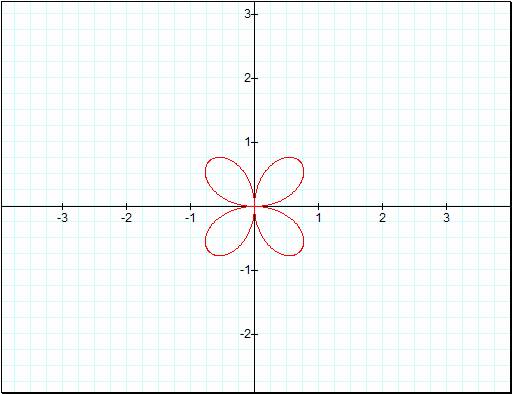
Now the second graph has
jumped passed the first one in the fact that we now have 4 leaves in our second
image while the first graph just has two leaves. But notice that the second graph
is still smaller than the first one. Let’s take it up again by a value of 1.
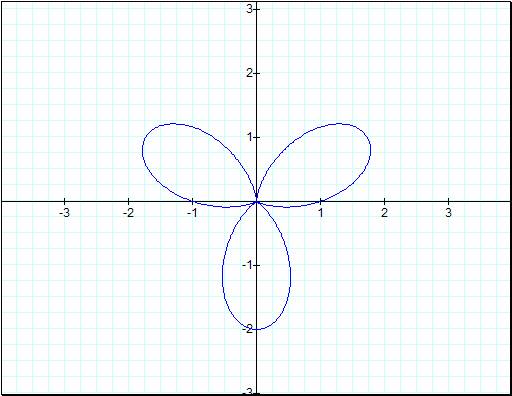
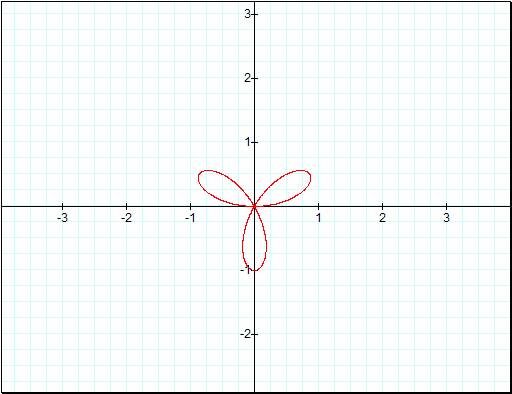
Now we can see that it is
basically the same shape just scaled by some factor. Let’s do one more with a
value of 4 and see what happens.
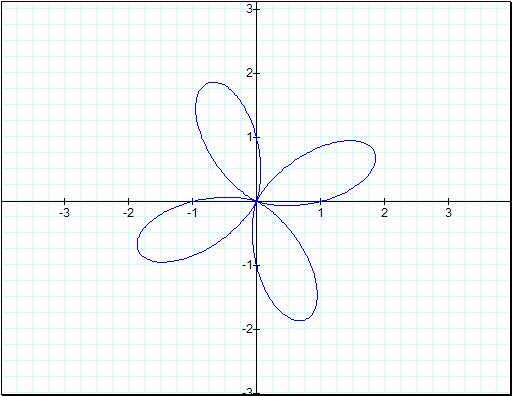
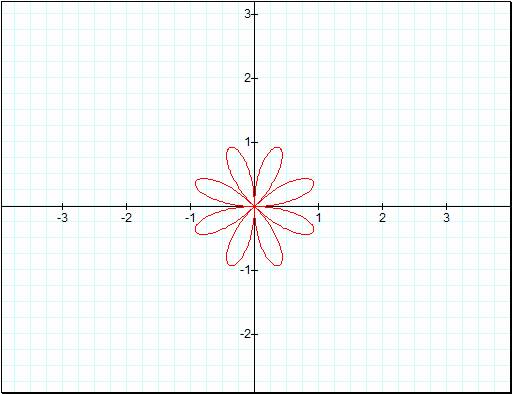
Now we can make a limited
conjecture that when the value of k is even then the graph of will have twice as many leaves, and be smaller
than the graph of with the values of a
and b equal to one. And when both of the k’s equal an odd number then they will
have the same leaves but again will be smaller.
Now that we’ve looked at the
values of a and b at 1 let’s suppose a and b are equal to 2.
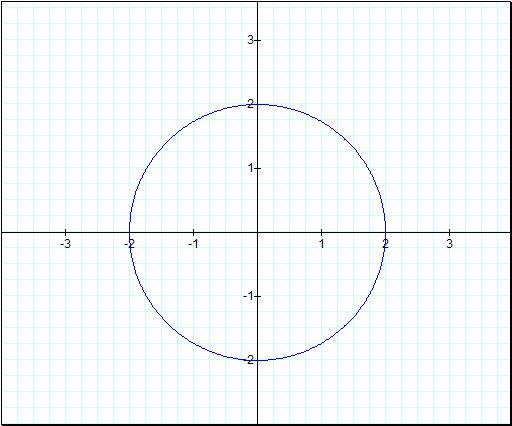
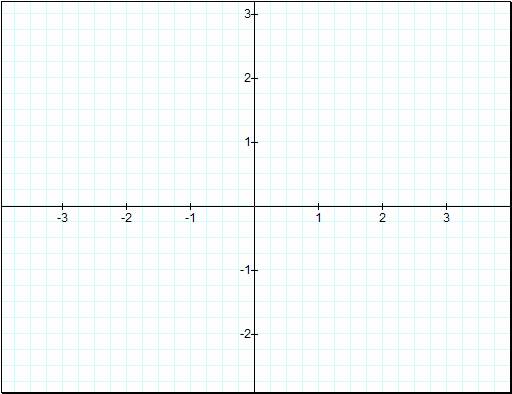
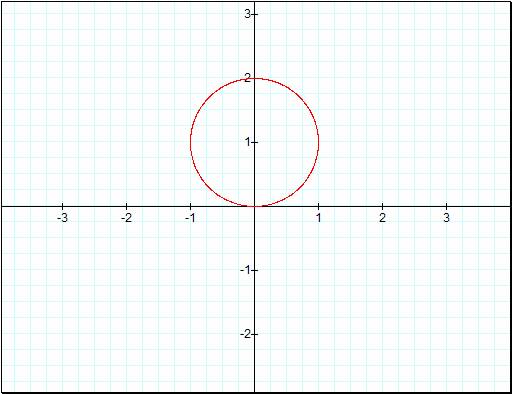
Once again we get a circle with
radius equal to a in the first graph and nothing in the second graph because,
again, sin(0) = 0. So let’s do the same methods as before and increase k by 1.
Again we get a cardioid and a
circle respectively in our first and second graph. But it’s also no surprise
that the objects are twice the size as before. Can we assume that the values of
our earlier graphs hold true in these next examples, and can we guess that they
will all be twice the size as before?
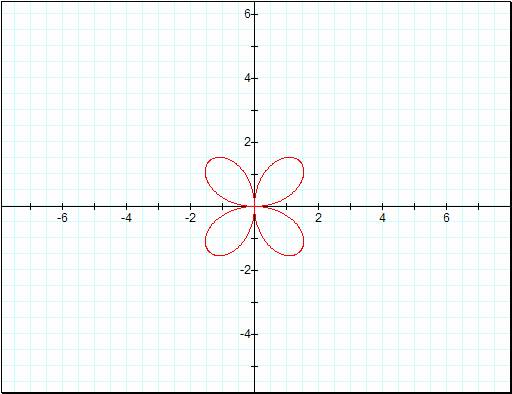
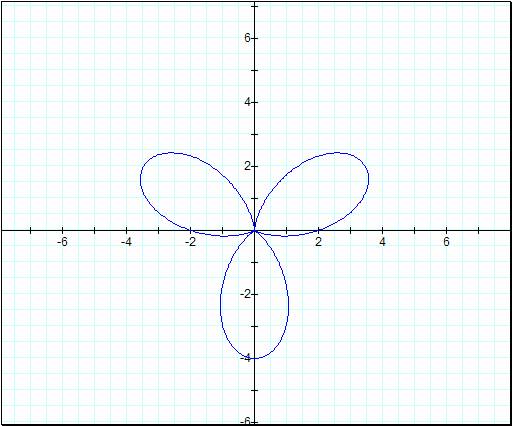
Do these look like they are
twice as big as before? Don’t let your eyes be fooled. I had to shrink graphs
to fit the images inside the picture box. They are in fact twice as big as the
ones previous. So can we expect that this will hold true for all our graphs?
The answer is yes, and we’ll do one more to show you.
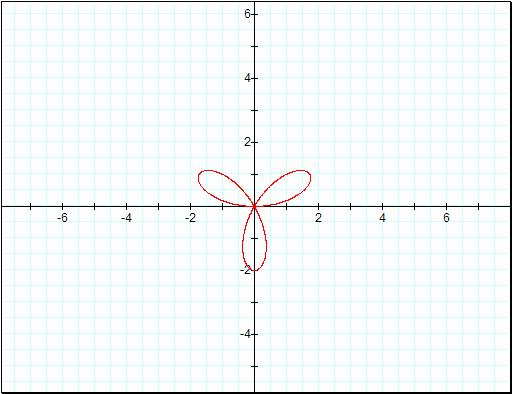
Here are some cool looking
designs with our equations. This one is our equation and the values of a and b
are increasing from 2 to 10 in even intervals. Red is 2, yellow is 4, blue is 6,
black is 8, and gray is 10.
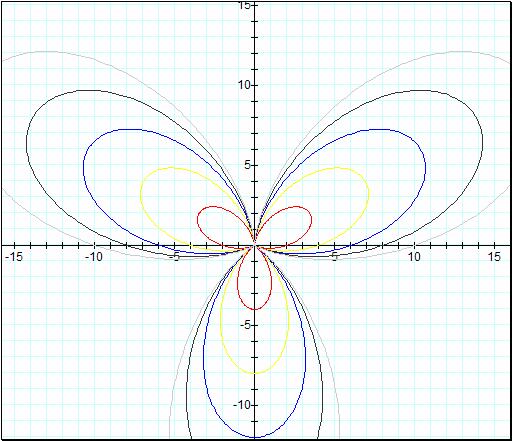
In this one below we have our
second equation with b increasing from
1 to 6.
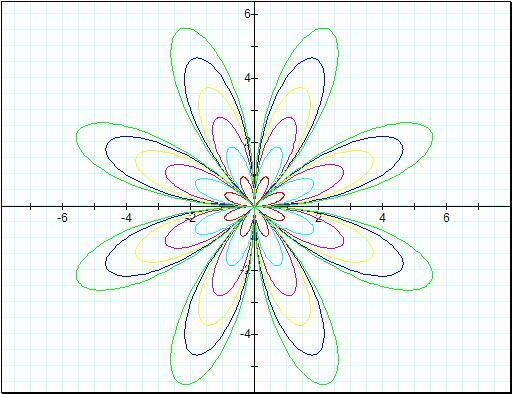
Perhaps this is where the
term N Leaf Rose comes from?
One might wonder about the
cosine function and it’s involvement with all these values. Can we expect the
cosine of each of these equations to act in the same fashion? Let’s do a few
quick observations to find out.
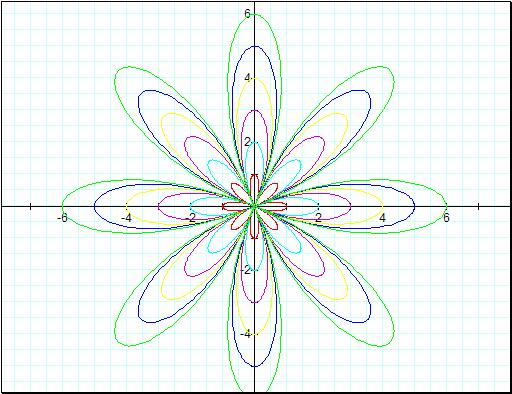
All we did on this graph is
make the sine a cosine function. So now we have 
where a is increasing
from 1 to 6 in succession. Notice that we still have eight pedals in our
flower, but they have rotated. It turns out that our cosine function is just a
phase shift of our sine function and the shapes have stayed the same. So if you
went back and did all this over again with the cosine function you would arrive
at the same conclusions. In fact if you’re curious and you have some time click
on these four links to do you own investigation with cosine and sine. Just
click on the equations and the links will be there.
Verses 
And
Verses 
Write Up by David Drew