Assignment 12: How good is your Guitar Really?

By: David Drew

EMAT 6680, J. Wilson

 

 

Have you ever been playing your guitar and stopped to wonder why it is shaped like it is? When you started tuning it have you ever been curious as to why the frets are different lengths and why they become closer together as you go higher up on the fret board? Hopefully we can answer some of these questions with a ruler and Excel which we use to, graph the function for us.

 

 

For this discussion I’ll be using my next door neighbor’s guitar. His name is Taylor Fletcher and he plays in a band based in Athens called the Happenin’. They’re excellent musicians and I suggest you check them out here at they’re website. His guitar is a Custom Gibson Les Paul with a sunburst top and pearl block inlays on the frets. I decided not to use mine simply because I wanted a much nicer guitar to work with. And as everyone knows, nothing plays like a Gibson. Here’s a picture of a similar guitar, but Taylor’s has a sunburst finish on the top.

 

 

Here’s the method I used to measure this guitar. Place a ruler at the very edge of the guitar where the neck meets the fret board. We’ll call this the 0 fret. Measure from the 0 fret to the bottom side of the last metal bridge, called the 22 fret. Here’s the numbers that were produced from the Gibson. And here’s the link to the Excel Spreadsheet. Les Paul

 

Frets

 

Lengths in Inches

Ratio

 

0

 

17.75

0.919014085

 

1

 

16.3125

0.921455939

 

2

 

15.03125

0.916839917

 

3

 

13.78125

0.916099773

 

4

 

12.625

0.913366337

 

5

 

11.53125

0.910569106

 

6

 

10.5

0.907738095

 

7

 

9.53125

0.904918033

 

8

 

8.625

0.898550725

 

9

 

7.75

0.89516129

 

10

 

6.9375

0.882882883

 

11

 

6.125

0.887755102

 

12

 

5.4375

0.873563218

 

13

 

4.75

0.855263158

 

14

 

4.0625

0.846153846

 

15

 

3.4375

0.836363636

 

16

 

2.875

0.804347826

 

17

 

2.3125

0.783783784

 

18

 

1.8125

0.724137931

 

19

 

1.3125

0.666666667

 

20

 

0.875

0.5

 

21

 

0.4375

0

 

 

 

 

0.807483243

Average

 

And here’s the chart to give you an idea of what the relationship is like.

 

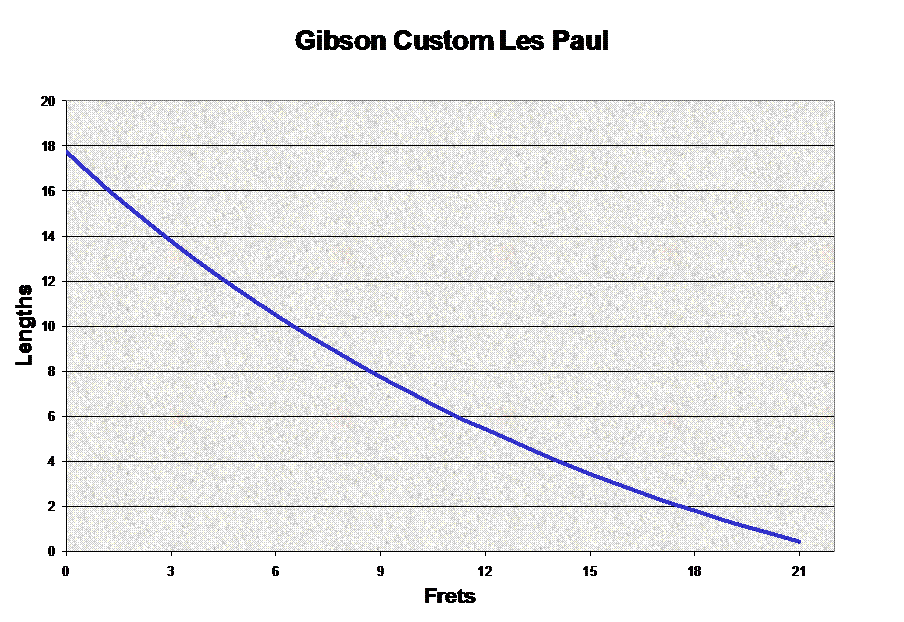
So now that we have a relationship on our graph, can we create a function that will give us this relationship? More specifically, is there a formula for the frets of a guitar? Let’s explore this with our values from our measurements and Graphing Calculator. First we need to add a graph of the ratios from one fret’s measurement divided by the measurement of the fret directly above or before it on the fret board.

 

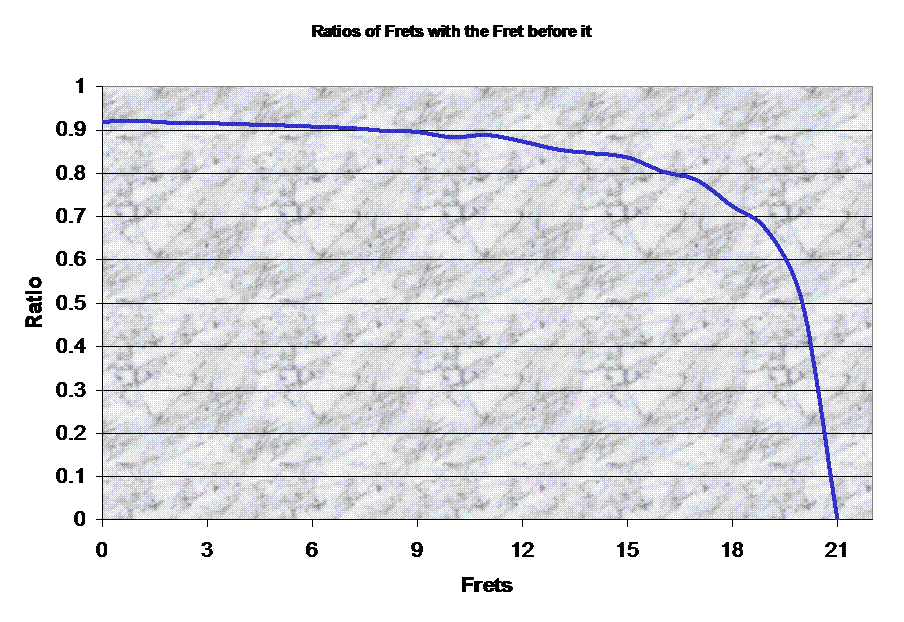
This graph looks surprisingly familiar, and it turns out if we graph the function 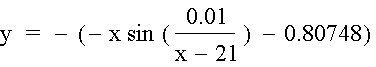 and restrict it on the interval x = < 0, 21 > then we’ll have a function that resembles our graph in Excel. Here’s a picture and a Link.

 

 

As you can see we have a “table like” graph from 0 to around 20. But as the frets become smaller and smaller their ratios begin to drop off the table and go into negative infinity at a drastic rate. Since we only have 22 frets, the graph will have a limiting value at 21 with a vertical asymptote at a value of 21, as you can see. This is true because although there are 22 frets we’ll only have 21 measurements, hence the limit will be at 21. I came up with this equation by several trial and error methods. Finally I concluded that we should have a value of 0.01 over the (x – 21 frets) so that the table wouldn’t drop off too soon. And we used 0.80748 because it was the arithmetic mean.

 

We do notice that the graph of the Gibson is a bit wobbly from frets 9 to 18. What does this suggest? I’ll make a conjecture, but I’m not sure if it is correct because I know very little about making guitars. The wobbles could indicate a human error in my measurements or it could indicate that the guitar was made with human hands and hence is infinitesimally flawed in its construction. Or perhaps, neither one of these assumptions are true and this is the way that the guitar was supposed to be created due to the differences in the notes and the abnormalities in the B and E frets and their relationship with the sharp notes. Since there is no B or E sharp then there is only a half step from B to C and another half step from E to F. And in fact these half steps are located at the 7th to 8th frets, the 12th to 13th fret, and the 19th to 20th frets respectively. And if you look carefully at the Excel graph of the ratios, you can see the biggest dips come around the 8th, 12th, and 20th frets.

 

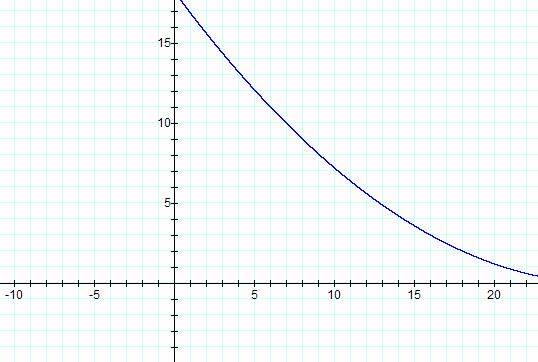
If we go back to our graph with the lengths of each fret to the end of the fret board can we find function to match that graph? It looks like it has the properties of a parabola opening upward. So, again, by trial and error we find that the equation 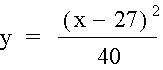has the same rough look as our Excel chart. Here’s a picture and a link.

 

 

 

In conclusion we can say that there is in fact several different ways to graph the function of a guitar’s fret board. And I’ve made a few conjectures and assumptions about why there might be inconsistencies in the graph. If you’re interested in the real art of making guitars then go to any or all of these sites.

http://www.bourgeoisguitars.com/

http://www.olsonguitars.com/

http://www.kbguitars.com/

http://www.warriorinstruments.com/default2.asp

 

 

Write Up by David Drew

Back Home