
Assignment 4: What is the Euler Line?
By: David Drew
EMAT 6680, Jim Wilson
As a current student and a future teacher there are several
things that I feel I should know like the back of my hand. And when I run
across a term or certain equation that I don’t know or understand then I like
to explore it until I feel I have mastered it. In this case I would like to
take part 5 of assignment 4, and adapt it to fulfill my curiosity. I have heard
the buzzword ‘Euler Line’ several times in my first few classes in
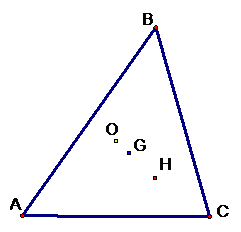
We start with any triangle constructed from points A, B,
and C. As shown below.
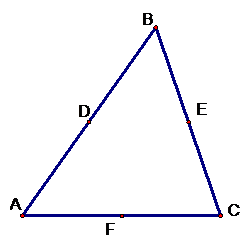
Now we make the medians of each segment so we have points
D, E, and F bisecting segments AB, BD, and AC, respectively.
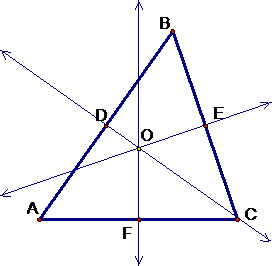
Now we’ll begin to create to Euler Line. Before we can say
that we’ve constructed the Euler line we need to find three very important
points inside the triangle: the centroid, the circumcenter, and the othocenter.
These three points are critical and intriguing, but this is an assignment about
the Euler Line and thus I will only give a small definition of each of these as
well as a picture for visual effects.
Centroid: A line connecting a vertex with the
opposite side’s midpoint is called a median of a triangle. If we construct the
three medians then we can see that they all intersect at a certain point. This
point, as you’ve guessed, is the centroid. It’s represented by the point G.

Circumcenter: The lines through each median D, E,
and F parallel to their corresponding segments intersect at a point O. This
point represents the center of the circle that the three point all lie on. This
is known as the circumcircle.
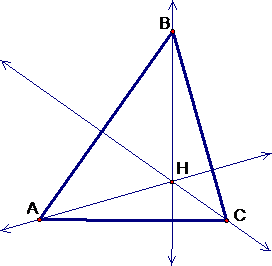
Orthocenter: An altitude of the triangle is a line
drawn through a vertex perpendicular to the side of the triangle opposite the
vertex. There are three altitudes: one is AD perpendicular to the side BC, the
second is BE perpendicular to the side CA, and the third is CF perpendicular to
the side AB. The altitudes of a triangle meet at a point, called the
orthocenter, denoted here by H.
We have all the ingredients for the Euler line so let’s see
the final product when the centroid, the circumcenter, and the orthocenter are
all together.
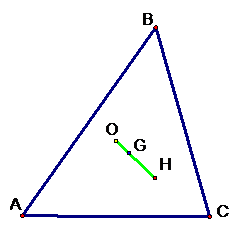
As we can see the three points seem to lie on one distinct
line. This line is the famous Euler Line. Here’s final picture with the line
connecting all the points.
Here’s a quick and simple proof of the Euler line. We’ll do
this proof and then say some things about Euler after and call it quits on our
discussion.
Proof: We one last picture to demonstrate our theory
about the Euler line. We are just going to include the midpoints of each
segment of our original triangle.
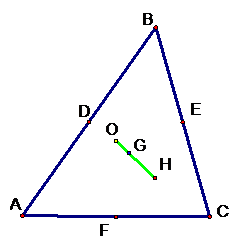
We’ll take a closer look at triangles ACB and EDF. As you
can see triangles ACB and EDF are similar, and EDF is half the size of ACB.
Concordantly DE is parallel to AC, DF is parallel to BC, and EF is parallel to
AB since each of the points D, E, and F are all midpoints of their
corresponding segments. These triangles are called parallel triangles or
homothetic triangles if you wish to use the more scholarly term. We also know
from above that AE, CD, and BF all meet at point G. But we also know that ACB
is a scale of EDF with a factor of -2 over G. This means that if you take a
point T on EDF, measure the distance TG, multiply TG by 2 and go that distance
on the opposite side of G, you’ll get the corresponding point S on ACB.
Now EO is perpendicular to BC, from our construction of O
above, but since BC and DF are parallel then EO is perpendicular to DF also. In
this way we can tell that O is the orthocenter of EDF. And thus we have an
interesting observation: the circumcenter of ACB is the orthocenter of EDF. Now
we can see what happens when we multiply the orthocenter of EDF over G with a
factor of -2. The solution must go to the orthocenter, H, of ACB. So when we
perform this scale of our point O we get H of the big triangle ACB therefore
all three points must be on one line, Euler’s Line.
For your own exploration of the Euler Line you can click here.
For your own fulfillment here are some links about Euler
and his work:
Writer’s Note: This write up was
written entirely by David Drew, but it would be foolish of me not to give
credit to several people for helping. I’d like to credit Dr. Floor for the main
proof of the Euler line, and Dr. Wilson and Dr. Rothestein of UGA for various
constructions and explanations.