
Assignment 7: Tangent Circles and the Ellipse
By: David Drew
EMAT 6680, J. Wilson
††††††††† We begin this investigation by saying that many things in
this world are guided by conic sectionís principles. And as we remember conic
sections are defined to be circles, hyperbolas, ellipses, and parabolas. There
are conic sections in virtually all aspects of our daily lives. Parabolas are
the main method for making headlights in our cars, and binoculars to watch
football games with. And ellipses are the guiding force that makes our world
rotate around the sun without shooting off into space, which makes this section
the most interesting. Iím basically going to take a tweaked view of problem 6,
which investigates the locus of the centers of the constructed tangent circles
with two given circles one on the inside of the other.
We
will now start by a creation of a circle that is tangent to two other circles
one being on the inside of the other.
1.
Start by making two distinct circles one inside the other and without them
touching.

2.
Next we need to mark off a point on the larger circle where we can construct
the smaller circle with the radius on the larger circle. And then we make a ray
from the center of the larger through the center of our constructed circle,
with the intersections of the ray and the constructed circle labeled.

3.
From here we take the intersection on the outside of the large circle and we
connect it with the radius of the original smaller circle. After weíve made
this segment we find the midpoint and drop a perpendicular of the segment
through the midpoint. And hopefully this perpendicular will intersect with our
ray.

4.
If we hide everything and construct another circle at our newest intersection
point and we have the radius extend to our point on the larger circle we should
get a circle that is tangent to our first two circles.

Our
construction turned out to be correct and if youíre not convinced and youíd
like to investigate then be my guest and click here.
Warning:
Hereís where our investigation takes an elliptical bend (no pun intended).
If
we stay with our construction from above then all we need to do is construct a locus
by selecting the point on the edge of our larger circle followed by the center
of our tangential circle. And the locus should look like this.
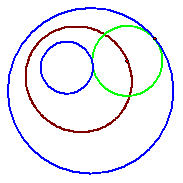
Now
the trick is to prove that this construction is in fact a real ellipse. We need
to do this because although we may trust GSP and our eyes we still may see
something that actually isnít there at all. So letís begin with the proof.
First we need to label our points to make an elegant and concise proof.
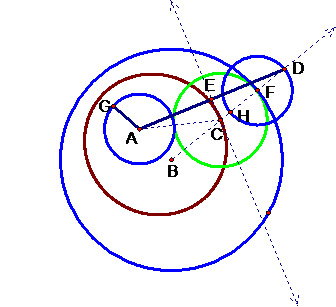
If
we say that A and B are the foci of the ellipse then by the definition of an
ellipse the distance from A to some point C on the ellipse plus the distance
from B to the same point C is a constant. We begin the proof by saying that BD
is a constant because it is the sum of BF (our large circleís radius) plus FD
(our small circleís radius, which is equal to GA). So the first part of our
ellipse, BC, is just BD minus CD, which turns out to be the radius of our
smaller circle plus the radius of our tangential circle. This length, CD, is
not constant, but fortunately for us it is congruent to some other piece of our
picture. It turns out that triangle ACE is congruent to triangle DCE, and Iíll
show you why. We constructed segment AD, found the midpoint, and called it E.
So E bisects AD and therefore AE is congruent to DE. We also constructed the
line through EC by dropping a perpendicular with AD through E, which makes both
angles AEC and DEC right angles, and hence these angles are congruent also.
Finally both triangles share a side CE. So by the side-angle-side axiom we can
say that triangles ACE and DCE are congruent. Therefore AC must be equal to CD.
And as we said before BC plus CD is a constant and by our definition of an
ellipse, and thanks to the SAS axiom we can say that AC + BC is a constant
length.† Through all this we learn that
our locus of construction is in fact an ellipse as we had theorized.
The following picture is what
happens it our smaller circle moves out of interior of our larger circle. Can
you guess that happens to the locus without looking at the picture?
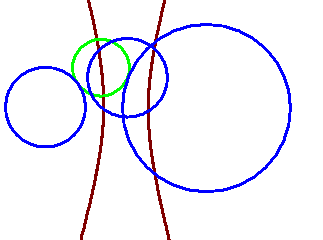
If you guess that it would
create a hyperbola then you guessed right. Or it could be the case that you saw
the picture before you even read the question. Whatever the case may be, the
real question comes as an aside to the above proof. Can you prove that the
locus created here is in fact a hyperbola? I wonít give a rigorous proof here,
but remember that the constant is not a sum but a difference between two points
on the hyperbola, and if you include an absolute value sign then youíll get
both branches just like our picture. You can mess around with that construction
here.
To conclude our discussion on
the Elegant Ellipse I have included a GSP file of the Earth rotating around the
Sun. This is really how the orbit works, and how many orbits work through out
our solar system. The Sun acts as a foci and the other foci is somewhere out in
space. Whatever the case may be itís fun to watch this demonstration so click
on Earth and Sun to view it. Also click on Gears to view a GSP demonstration of how
elliptical gears work.
Write Up by David Drew. All
work is credited to the author who is particularly happy with the Elliptical Gears
Construction.