
Assignment 8: The
By: David Drew
EMAT 6680, J. Wilson
We want to investigate the
nine point circle, its history, and eventually make a conjecture and give a proof
of our assumption. So let’s begin with a triangle and show how we get the nine
point circle.
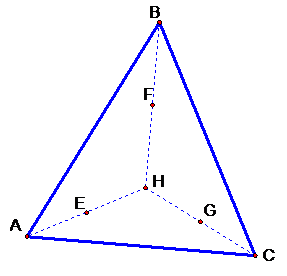
Given any triangle ABC we
start by finding all the altitudes of the triangle. Theses lines are the lines
that pass through a vertex and are perpendicular to the side opposite of the
given vertex. We label their intersection H, or the orthocenter. We now make
segments AH, BH, and CH and find the midpoints of all those segments.
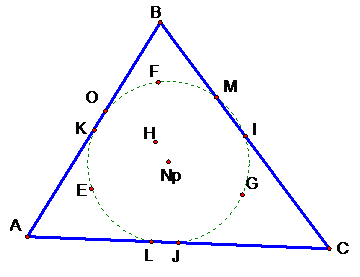
Next we find the midpoints of
AB, BC, and AC and construct a triangle out of those three points. We make a
circumcircle from our ‘midpoints’ triangle and we have the Nine Point circle.
The points on the circle are as follows: the midpoints of the segments of our
original triangle, the intersection of our altitudes and the sides of our
triangle, and the midpoints of AH, BH, and
Now that we know how to build
the Nine Point Circle can we make any conjectures and back those up with
proofs?
Click on Nine Point to move or shift the circle around.
We’ll go with an interesting
observation from my own investigation and try to realize how and why it is
true. The four circumcircles
of points in an orthocentric system taken three at a time have equal radius.
Now that we’ve stated this
theory we need to go back and define a few vocabulary words. An orthocentric
system is given by the picture below and here on
GSP.
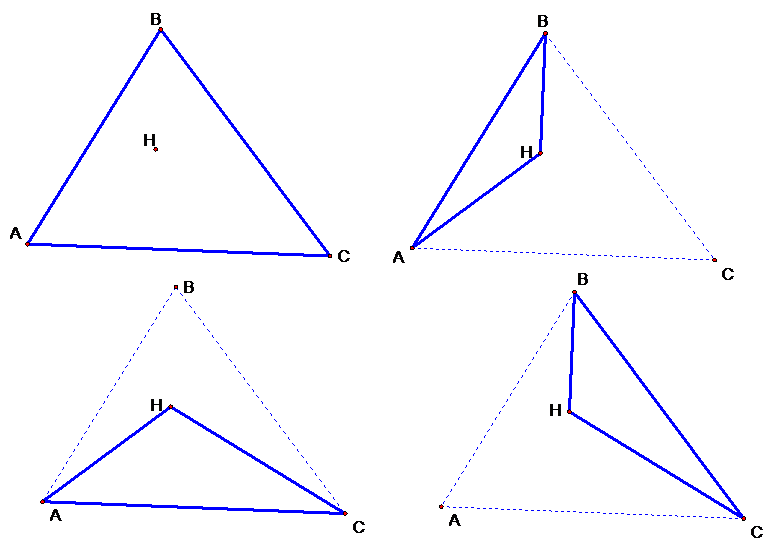
It’s simply the four sets of
triangles given by one triangle A, B, C and its orthocenter, H. According to
this picture there are four such different combinations, and all of their
circumcircles have an equal radius. To condense the picture I’ve located all
the circumcircles onto the original picture to give us this image.

Now comes the trick of
showing that all these circles have the same radius. Click on Circumcircles to look at GSP and the measurements.
But since we can’t use GSP as a tool of proof then we need to show some
geometric congruence’s. First of all what do we know about all the outer or
excircles? They all pass through point H by their construction so XH is a
radius, ZH is a radius, and YH is a radius. But we know that by our
construction points X and Y are one a line that is a perpendicular bisector of
AH that crosses AH at point E. So XE is congruent to EY. And the two triangles
share a side of EH as well as a ninety degree angle at E so by the Side Angle
Side axiom XH is congruent to HY. And since YZ is on the same line which is a
perpendicular bisector of HC through D then YD and ZD are congruent. And if we
go through the same logic as before we will come to another SAS axiom that HY
and HZ are congruent so all of the radii of our three outer circumcircles are
the same. And since we know that X, Y, and Z are just reflections of the
orthocenter of our original triangle we can say that its radius is also
congruent to the other three. So our assumption that all the circumcircles in
our orthocentric system are the same is true.
As promised here is some
history of the Nine Point Circle. History
And here are three nice
proofs that I found on the internet. Proofs
Write Up by David Drew