
Assignment 9: Pedal Triangles and ‘Homer’ Simson’s
Line
By: David Drew
EMAT 6680, J. Wilson
Our investigation begins with any simple triangle ABC in
the plane and some point we’ll label P anywhere on the plane also.
The first thing we need to do is demonstrate how you
construct a pedal triangle. After we have done this then we can discuss the
various positions of P and the decompositions of our pedal triangle.
Since our point P can be anywhere on the plane (and we don’t
want to have an inconsistency with our lines) we need to extend the triangles
sides with lines through AB, BC, and AC. And we construct the perpendiculars of
each of those lines through our point P. Here’s a picture to keep you up to
speed.
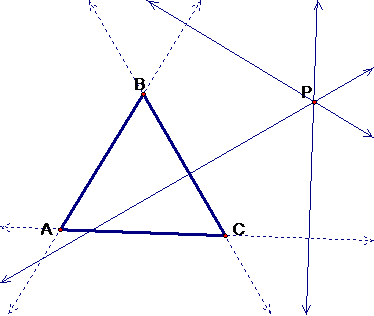
There are several lines and it may be confusing to look at,
but we have extended our triangle with the dashed lines, and we’ve created
perpendicular lines through P with the thin lines. Now we need to label the
intersection of our perpendicular lines with the extended triangle lines. We’ll
label them D, E, and F.
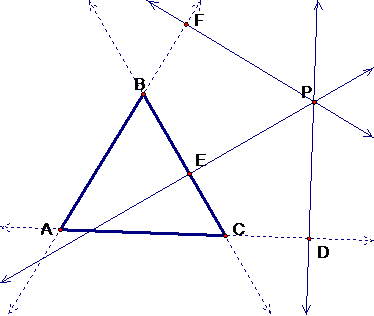
And if we clean it up a bit and make a triangle out of D,
E, and F then we’ll have our pedal triangle.
For those of you who don’t have GSP let me show you a few
examples of what happens when you move P about the plane.

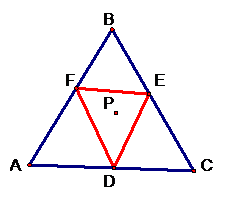
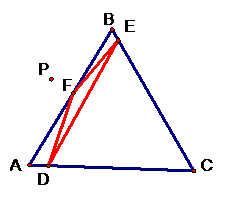
For those of you with GSP click on
Pedal to move P around yourself. Pedal
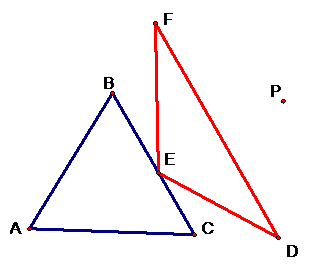
There is an interesting thing happening if you can position
P in the correct place. There is place you can locate P in which our triangle
isn’t a triangle. The new creation we’ll have in this case is a straight line.
It might not be perfectly straight but here’s a picture of the decomposition of
the triangle.
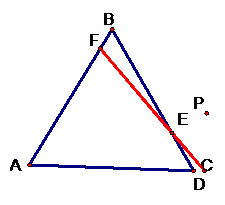
It turns out that this decomposition is called the Simson
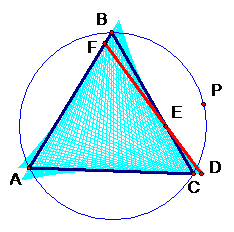
Line. But we know a trick to let us get the exact Simson Line. First we
construct the circumcircle or our original triangle ABC. And next, with the
help of GSP, we merge our point P onto the circumcircle. Here’s a picture.

By definition from Mathworld the Simson Line is ‘the line containing the feet P1,
P2, and P3 of the perpendiculars from an arbitrary point P
on the circumcircle
of a triangle
to the sides or their extensions of the triangle.’ So in essence
we cheated a little by knowing that this would work, but there are still a lot
of cool things we can do with the Simson Line. Here are some interesting
observations on the Simson Line. Click here to mess around with Simson’s Line.
The Simson line bisects the line HP, where H
is the orthocenter
(Honsberger 1995, p. 46). Moreover, the midpoint of HP lies
on the nine-point
circle (Honsberger 1995, pp. 46-47). The Simson lines of two
opposite point on the circumcenter
of a triangle are perpendicular
and meet on the nine-point
circle.
Here’s a picture of what all
this looks like.

But the neatest thing about the Simson Line is the Locus it
makes in relation to point P. This is also from Mathworld, but I think it fits
nicely. ‘The envelope
(or locus) of the Simson lines of a triangle is a deltoid. The area of the
deltoid is half the area of the circumcircle, and Morley's
triangle of the starting triangle has the same orientation as the deltoid. Each side of the
triangle is tangent to the deltoid
at a point whose distance from the midpoint of the side
equals the chord of the nine-point
circle cut off by that side. If a line L is the Simson line
of a point P on the circumcircle of a triangle, then P is
called the Simson line
pole of L. Here’s the last picture of the locus. Click here
to play around with the Locus.
In conclusion I just want to say that there are so many
relationships among a lowly triangle. From the last few assignments we’ve seen many
constructions, envelopes (or loci), and decompositions. The world of triangles
is a vast world full on wonder and exploration that is waiting to be tapped
into. I wrote this assignment solely by myself. But I did have a little help
from Mathworld and Jim Wilson on a few of the constructions.
Write Up by David Drew