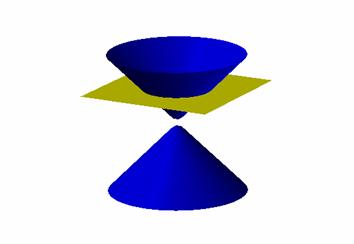
Conic Sections: A First Lesson
We begin by
asking the question what is a conic section? Moreover what is a conic? A conic
is simply two cones merged together at their tips to create a double cone shape.
Imagine two ice cream cones touching at the bottom and facing away from each
other. Here’s a picture to illustrate.
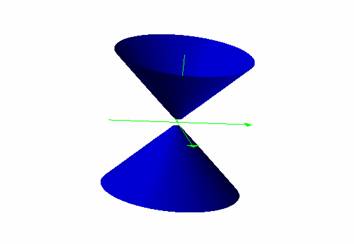
As you can see
the conic is really a simple shape. The radius of a section of the cone is
simply equal to the length of the z-axis. In this case our equation is given by
. If you are not
familiar with the z-axis then here’s a quick run down…The z axis is just the
height of an object in the Euclidean Plane. Imagine if you placed a Rubik’s
cube on a sheet of paper, obviously you can trace the bottom of the cube and
give it x and y coordinates if you wanted to. But these traces would not be the
cube or even an accurate description of what the cube looked like. You would
need to introduce a new element or the z axis to finish off the description of
the cube. So as I said before the z axis is just the height of an object or the
measurement of the third dimension. With that said now we can turn our
attention to what happens when we cut the cone with a plane, or in other words
how can we divide the cone into two different pieces?
The first
section is the easiest to describe because it cuts the cone parallel to the
Euclidean Plane to create a circle.
|
|
|
As you can see
the plane which is just the z plane cuts the cone to give a circle where the
cone and the plane meet. The equation to create the plane is given by n = z,
where n can be any real number. Remember the cone can go on expanding until
infinity so it theory we can place a given plane with any real value (positive
or negative) to slice the cone. Now we move onto the next section.
If we have a
circle when the z plane is parallel to the Euclidean plane then what happens
when we tilt the z plane slightly? The answer is we get a new conic called an
ellipse. The ellipse is a fascinating part of many of our everyday lives and
there is even another lesson devoted solely to the ellipse. Here are the
pictures of the slice creating an ellipse.
|
|
|
Notice that the plane has a different slope than the conic.
In general the conic goes on forever so in general as long as the plane has a
slope of less than the conic and not the same we will get an ellipse. It turns
out that if the slope is the same or more than the conic then we will get
another section.
In fact if the
slope of the plane is more than the conic (i.e. if the plane slices the conic
on both ends) we have what is called a parabola. In this particular section the
slope of the plane is 2, which is double the slope of the conic. Here are the
pictures.
|
|
|
The last
section exists when the slope of the plane is the same as the slope of the
conic which is called a parabola. The parabola has the same shape as a hyperbola
except with only one tail. Here are the pictures to demonstrate.
|
|
|
All of these
different sections have fascinating properties, but for this two week
exposition we will only focus on the wildcard of the bunch: the ellipse. Since we
have an idea of what a conic section is and we’ve been exposed to Algebra II
and Geometry we can explore the various intricate parts of the ellipse. So
let’s go back to the homepage and start the lessons on the ellipse, and
hopefully this will help us examine the other sections in the future as a class
or by ourselves.