Drawing/ Creating an Ellipse
There are
several different ways to create an ellipse. We can use any of the technology
applications to help us draw an ellipse, we can use everyday materials such as
a piece of string or paper folding, and lastly we can use our minds and our
math abilities to draw an ellipse.
We start with
the equation 
and we
substitute different values for x,y with constants at a and b. This method, as
I said before, is sloppy at best when drawing an ellipse. So for this reason
we’ll stay away from this method and go on to using the string and technology
to draw ellipses.
The easiest
and most available method for drawing an ellipse is with two push pins, a
pencil, and a piece of string. We begin by trying the string at the two ends to
make a circle. Next we put the push pins into a wall or a desk and lay the
string around the pins. Lastly we put the pencil inside the string and pull it
tight around the pins. The trace that we produce will be an ellipse. Here’s a
picture.
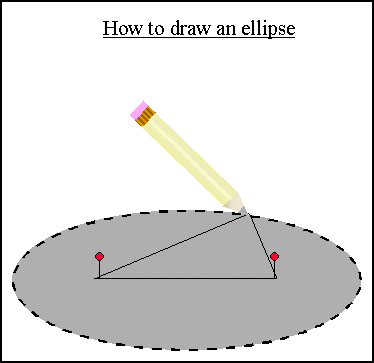
Several interesting questions arise from this picture such as
Why does the trace create an ellipse? Can you measure the distance from one
foci to another foci? And since the string is at a fixed ratio or length then
where does that fixed length come into play? These and other questions will be
addressed as we move forward in our exploration.
The second
method of drawing an ellipse is with some type of graphing software whether it
be Graphing Calculator or some type of TI-83 calculator. Either one will
suffice, but for this method I will use Graphing Calculator. If we set the
equation with a = 1.5 and b = 1 then we get a
picture that looks like this.
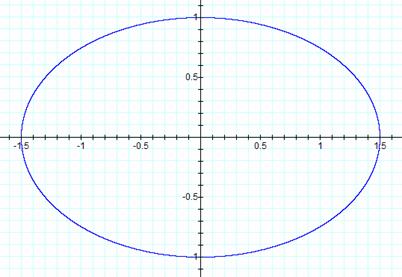
If we just let a and b equal the same value then we’ll get a
circle, which is an ellipse of a different form. A circle is an ellipse with
eccentricity equal to 1, but that will be later in the discussion of an ellipse
if we even get to it. Here’s an example of a movable ellipse on Graphing Calculator.
Just click the play button to watch it rise and fall depending on the
values of n. Can you make any conjectures or assumptions that may be involved
with this graph?
The last way
to create an ellipse is with Geometer’s Sketchpad. This, in my opinion, turns
out to be the most useful and the most interesting drawing of the ellipse. With
GSP we can create the ellipse and then move it and watch the changes occur in a
dynamic way. Here’s a picture of the creation as well as a detailed explanation
of how to make it on GSP.
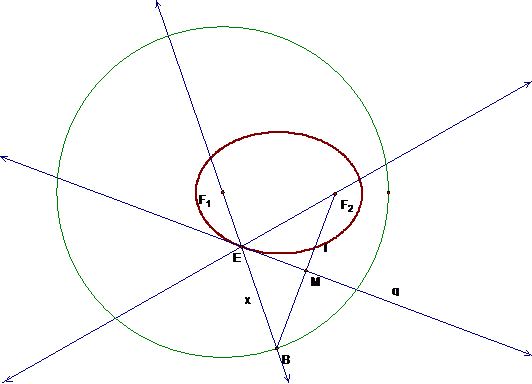
1. Start by
making a circle, C, with center F1.
2. Create a
point on the outside of circle C and label it B. Also place a point, F2
anywhere inside of the circle.
3. Make a
segment, l, from F2 to B and find the midpoint and call it M.
4. Construct a
perpendicular bisector with l, or a perpendicular line with l through M, call
this line q.
5. Now create
a line through M and F1 and call it x.
6. Find the
intersection of q and x and make a line through it and F2, call this
intersection E.
7. Lastly,
select E and B in that order, and go to Construct and Locus to create the
ellipse.
Now we have an ellipse that we can interact with. Click here
to play around with it. Ellipse