Proof that an Ellipse exists
Although we
have the string, Graphing calculator, and GSP to show us that we’ve created an
ellipse how can we be sure that our drawings are indeed a true ellipse? Well, I’m
not sure how we could provide an elegant method for the ‘String’ proof or a
concise method for our Graphing calculator, but I am positive that with GSP I
can give a very nice proof. Here are a couple of things to consider that I may
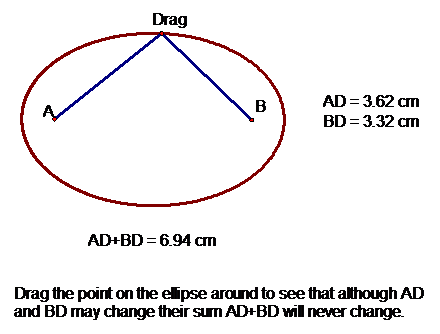
not have gone over. First of all the distance from the edge of the ellipse to
the first focus plus the distance from the same point on the edge of the
ellipse to the second focus is always a constant distance. Moreover wherever you
place this point on the outer edge of the ellipse will have this same property.
If you’re not convinced then click here for a GSP visual confirmation.
Here’s a visual for those of you that don’t have GSP.
The second
property that may be of importance in this proof is the fact that if an object
such as a sound wave or a ray of light passes through one foci then it will
reflect off the inside of the ellipse and at least pass through the opposite
foci. Here’s a picture to demonstrate.
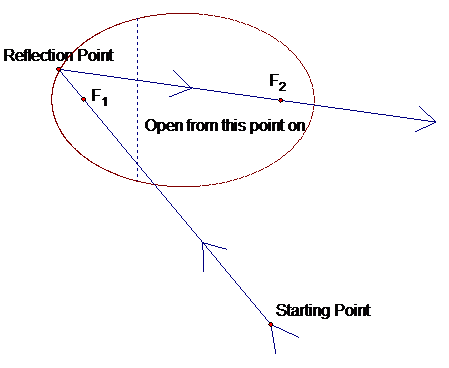
Suppose our
picture signifies a real ellipse with an opening starting at the dashed line
and having a reflective property to the left of the dashed line. Then as the
starting point of light ray goes through F1 and hits the reflection point it
will be shot directly to F2 and continue going away from F2 for ever into
infinity.
So with the
help of those two important properties we can discover a proof for the presence
of an ellipse. Although we may trust GSP and our eyes we still may see
something that actually isn’t there at all. So let’s begin with the proof.
First we need to label our points to make an elegant and concise proof.
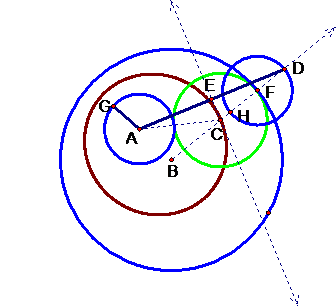
If we say that A and B are the foci of the ellipse then by
the definition of an ellipse the distance from A to some point C on the ellipse
plus the distance from B to the same point C is a constant. We begin the proof
by saying that BD is a constant because it is the sum of BF (our large circle’s
radius) plus FD (our small circle’s radius, which is equal to GA). So the first
part of our ellipse, BC, is just BD minus CD, which turns out to be the radius
of our smaller circle plus the radius of our tangential circle. This length,
CD, is not constant, but fortunately for us it is congruent to some other piece
of our picture. It turns out that triangle ACE is congruent to triangle DCE,
and I’ll show you why. We constructed segment AD, found the midpoint, and
called it E. So E bisects AD and therefore AE is congruent to DE. We also
constructed the line through EC by dropping a perpendicular with AD through E,
which makes both angles AEC and DEC right angles, and hence these angles are
congruent also. Finally both triangles share a side CE. So by the
side-angle-side axiom we can say that triangles ACE and DCE are congruent.
Therefore AC must be equal to CD. And as we said before BC plus CD is a
constant and by our definition of an ellipse, and thanks to the SAS axiom we
can say that AC + BC is a constant length.
Through all this we learn that our locus of construction is in fact an
ellipse as we had theorized.