Final Project: Final Investigation of the Lowly Triangle

By: David Drew

EMAT 6680, J. Wilson

The final project will be an exploration on several aspects of the triangle. Particularly it will investigate what happens if you connect the vertices of a triangle to some point P within the triangle. So without any more introductions let’s jump right in. We’ll have three parts to this final and we’ll label them I, II, and III.

Part I.

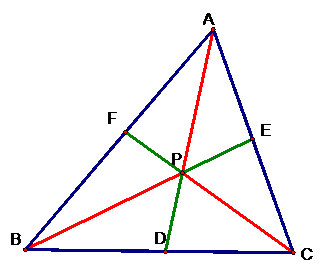
Consider any triangle ABC and a point P inside the triangle. We make segments AP, BP, and CP, and then we extend these segments to hit the opposite sides and label the intersections D, E, and F respectively. Here’s a picture to demonstrate the original idea.

Now we can explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P. Here are some pictures and here’s a file to let you investigate yourself. Triangle

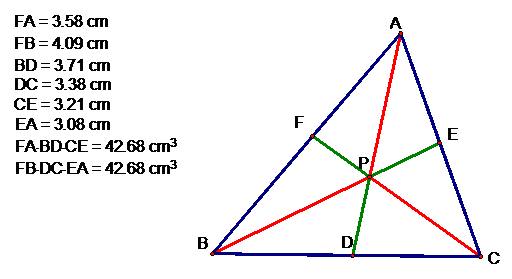
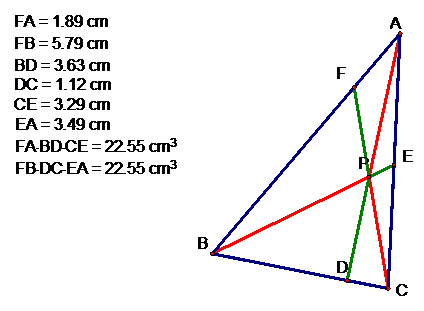
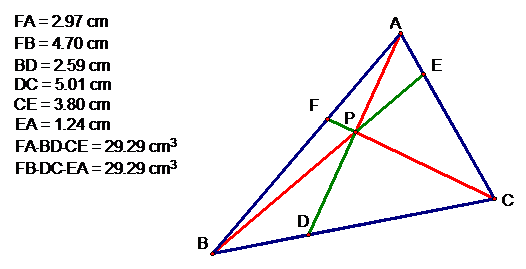
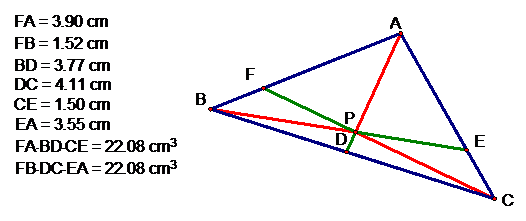
After just a few movements of P, as well as A, B, and C, we can tell that (FA)(BD)(CE) = (FB)(DC)(EA). So the ratio of these two lengths is one. .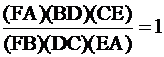

Part II. The conjecture and proof

Our conjecture is that 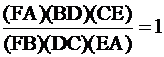. And now we need to do several things in order to prove this equality. Let’s

begin by constructing a couple of extra, but greatly needed, similar triangles. We’ll construct lines through B and C that are both parallel to segment AD. But we also need to extend a few lines so we can have an intersection. Here’s the finished product.

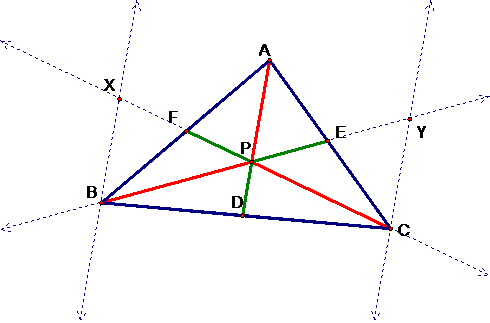
By alternate interior angles, and vertical angles we can say that if all the angles of two triangles are the same and their sides are in a fixed ratio with each other then those triangles are similar. So by our image above we can say that triangle XFB is similar to triangle PFA so 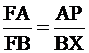. And also triangle YEC is similar to PEA so 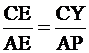. And by parallel

lines, common angles, and common lines we can say that triangles BDP and BCY are similar, and XBC is similar to PDC. So in the end after we’ve multiplied everything out we are left with the equation

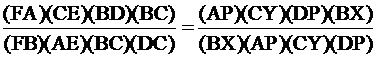. And as you can see if you reduce the second equation and cross the

terms out then we’re left with 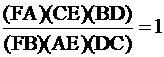, which is exactly what we wanted in the first place. But what

happens if the point P is outside our triangle. That’s no problem here’s a working GSP file that will let you explore the same relationships. Triangle 2

Part III.

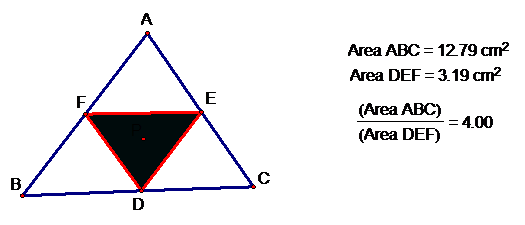
Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4? Here’s an investigation.

The triangles areas will always have a ratio of 4 or greater when looking at their two areas. And there’s only one place where the ratios are equal to 4. It’s when the point P is at the centroid of triangle ABC. Here’s a picture and the file Triangle Areas will let you place P wherever you want to locate it. Just keep P inside ABC.

Write Up by David Drew

Back Home