
Pedal
Triangles
(Assignment 9)
by
Cara
Haskins, Matt Tumlin, and Robin Kirkham
A Pedal Triangle is formed
from the following construction.
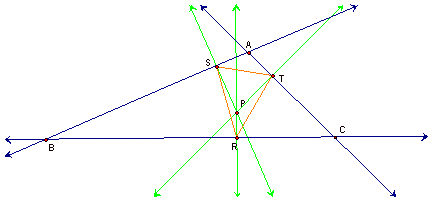
Let
triangle ABC, be any triangle. If P is any point in the plane, then
the triangle formed by constructing perpendiculars to the sides of ABC locate three points R, S, and T that are the
intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
First we will
examine triangle ABC with point P in the plane, and its perpendiculars
to the sides of ABC that creates the Pedal Triangle RST.
Now we will
examine what happens to triangle RST, if P is on the
side of triangle ABC:
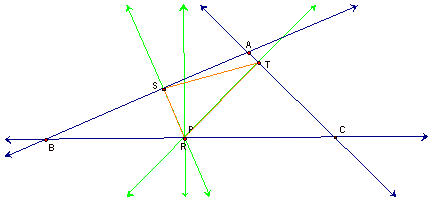
Regardless of where it is placed on the
side, you will notice that P becomes one of the vertices of
triangle RST.
Now let us
examine what happens with triangle RST, if P is placed at
one of the vertices of triangle ABC:
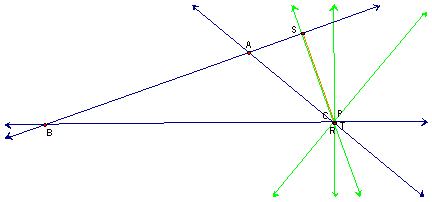
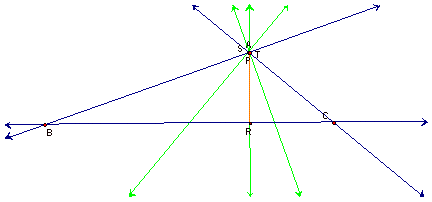
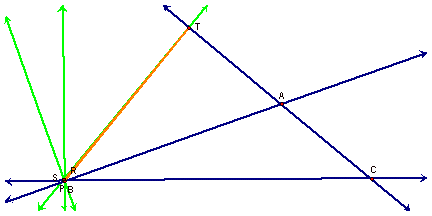
Regardless of
which vertex is used, you will notice that triangle RST collapses to
one of the perpendicular bisectors of triangle ABC.