
____________________________________________________________
Tangent
Circles
(Assignment 7)
by
Robin Kirkham, Cara Haskins , Matt Tumlin, and Audrey Simmons
____________________________________________________________
Let us consider the problem of having two circles whereas one is
inscribed within the other, and a third circle is constructed such that it is
tangent to both the original circles.
We are given :
Two circles
A point on one
of the circles
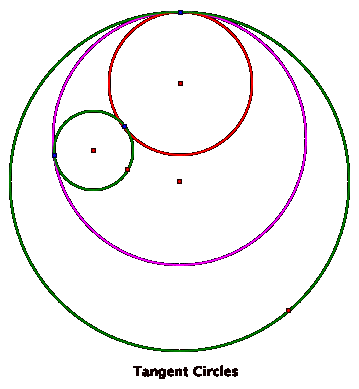
Let us start with two circles below shown in green.
We add the red circle inside the large green circle keeping it
outside of the smaller green circle. The red circle has been constructed using
the point on the outer circle.
When adding the purple circle tangent to the larger green circle
we observe that there is no tangency to the smaller circle. The purple circle is constructed to
circumscribe the smaller green circle.

To use the tangent circle script click HERE!
1. Loci of the centers of the tangent circles
Examine the loci of the centers of the red tangent circle. Can you
determine what shape would be graphed?
To see click HERE!
Examine the loci of the centers of the purple tangent circle. Can
you determine what shape would be graphed?
To see click HERE!
Observe that each set of the loci makes a separate ellipse.
2. Loci of the base of the isosceles triangle
Review the construction of the red tangent circle, the one that
was externally tangent to the little green circle (above).
Segment AB is the base of an isosceles triangle. It is
apparent that all points on the dotted red line are equidistant from both point
A and B since the line is the perpendicular bisector of AB.
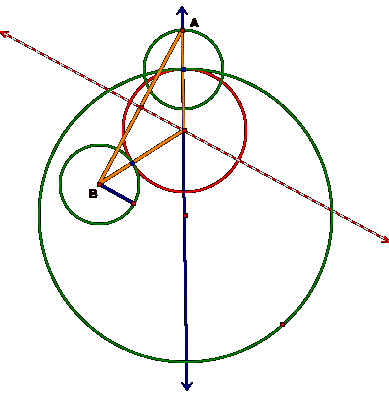
Can you guess what shape is made with the trace of the loci?
Instead of making an ellipse, the loci of the midpoints is a ________? (Try this and see)
Observe the locus of the midpoint of the segment by clicking HERE!
Can you guess what shape is made with the trace of the loci?
Instead of making an ellipse, the loci of the midpoints is a ________? (Try this is see)
Notice that the locus of the midpoints of the purple circle is
also the same.
The consistency of the arrangement of the points is quite
interesting.
Conclusion: In summary, the loci of the centers of the tangent
circles form ellipses. The loci of the midpoints of the bases of the isosceles
triangles (while under construction) form circles.