
Altitudes
and Orthocenters
(Assignment 8)
by
Robin Kirkham,
J. Matt Tumlin, and Cara Haskins,
An orthocenter (H) of a triangle is the point where the lines containing its altitudes are concurrent.
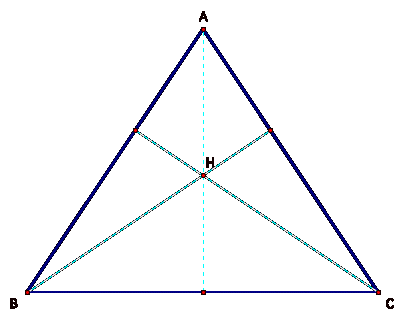
Now, let us
look at the construction of triangles between the orthocenter and 2 of the
vertices of the triangle.
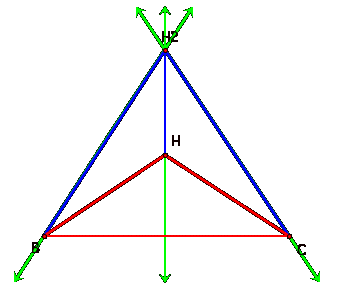
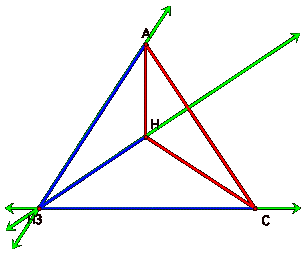
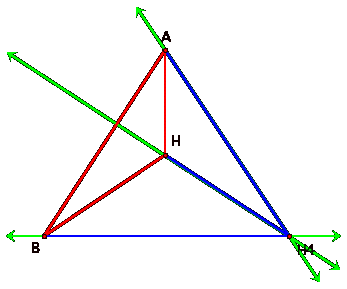
As you can
see, the orthocenters of the three triangles are the vertices of the original
triangle.
Does this
relationship hold true for triangle ABC given that a triangle may be acute,
right, or obtuse?
What would
happen if one of the vertices of triangle ABC was moved to where the
orthocenter (H) is located?
To use a
script tool to find out, CLICK HERE!
Now construct the Circumcircles for DABC, DHBC, DHAC, and DHAB.
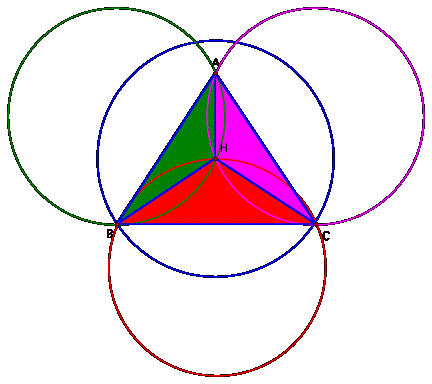
What can you
say about the radii of the circumcircles?
Are they congruent? Are you
sure?
To use a script tool to
move the points, CLICK HERE!
In conclusion some conjectures are:
á
The radii of the circumcircle is exactly the same.
á
All circumcircles pass through the orthocenter (H) of the original
triangle ABC.
á
A cube is formed by connecting the centers of the circumcircles
with the orthocenter (H). To use a
script tool, CLICK HERE!
á
The area of the overlap of the circumcenters at each vertex is
bisected by the altitudes of the original triangle.
á
A second area of the overlap of the circumcircles is bisected by
the sides of the original triangles.
á
We know that the perpendicular bisector that intersects each side
of the original triangle and travels through the orthocenter also intersects
one of the centers of the outside circumcircles.