Pedal Triangles

(Assignment 9)

by

Robin Kirkham, J. Matt Tumlin, and Cara Haskins

 

A Pedal Triangle is formed from the following construction.

  Let triangle ABC, be any triangle.  If P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC locate three points R, S, and T that are the intersections.  Triangle RST is the Pedal Triangle for Pedal Point P.

 

First we will examine triangle ABC with point P in the plane, and its perpendiculars to the sides of ABC that creates the Pedal Triangle RST. 

 

 

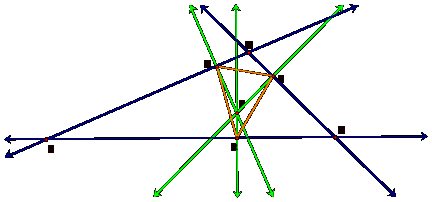
To use a script tool to move the point P around, click HERE!

 

 

Now we will examine what happens to triangle RST, if P is on the side of triangle ABC:

 

 

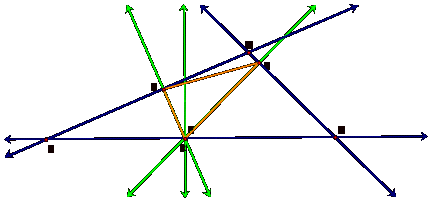
 Regardless of where it is placed on the side, you will notice that P becomes one of the vertices of triangle RST. 

 

To use a script tool to move the point P around the triangle, click HERE!

 

 

Now let us examine what happens with triangle RST, if P is placed at one of the vertices of triangle ABC:

 

 

 

 

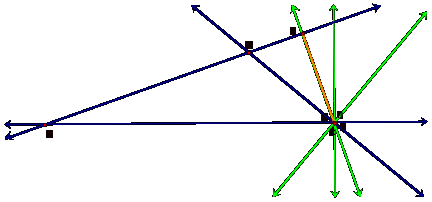
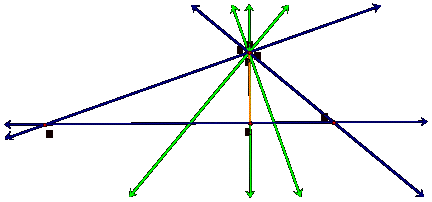
Regardless of which vertex is used, you will notice that triangle RST collapses to one of the perpendicular bisectors of triangle ABC.

 

 

Return to  RobinŐs Homepage