
Half the Area of a
Triangle:
A Line Parallel to the
Base
By
Robin Kirkham
This
is an investigation of the area of a triangle. This investigation shows the actual line that cuts the
triangle as well as some of the polygons that are created with the parallel
segment that was constructed.
Problem 1
Given
any triangle, construct a line parallel to the base and show that it cuts the
area of the triangle into one half the area of the triangle. This is done in figure 1 below.
Initially, this exercise
started as an analysis of this problem. Let us first look at the more obvious
division of the triangle.
Take a triangle and find the midpoint of two of the sides. Connect the two midpoints; notice that this is a segment that is parallel to the third side.
Figure 1
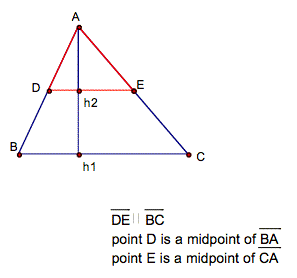
This makes ADE equal to 1/4
the area of ABC. This is not what
we are looking for. In order to
divide the triangle into two equal areas the construction of the parallel line
(in the above case is DE) is handled differently.
Let
us look at finding the method to find 1/2 the area of ABC. 1tri.gsp
1.
construct CBÕ=CB
2.
connect BBÕ
3.
construct midpoint M
4.
construct circle with
radius BM
5.
identify point N
6.
construct NP parallel to
AB
7.
construct PQ parallel to
CB through point P
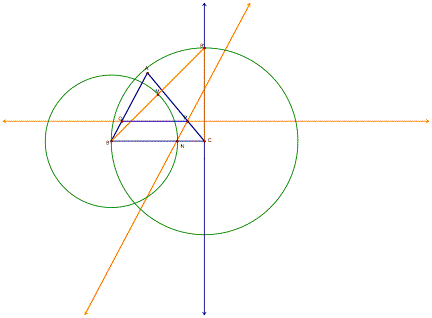
Hide the construction lines and you are left with the following:
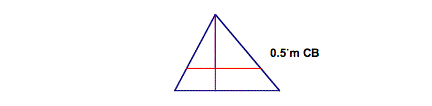
It may be interesting
before this triangle is divided into several polygons; we first take a look at
the different ratios that result from the two similar triangles.
Let us look at some of
the ratios:
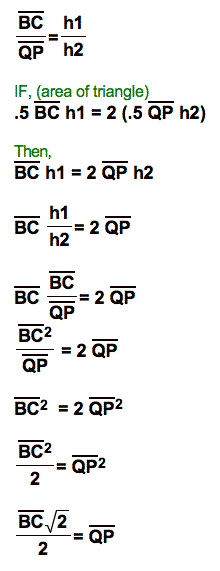
Problem 2
If the parallel segment that divides the triangle into
two equal areas is drawn for each base, a smaller triangle is formed.
A. What is the ratio of the area of the
small triangle to the original triangle? Interiortri.gsp
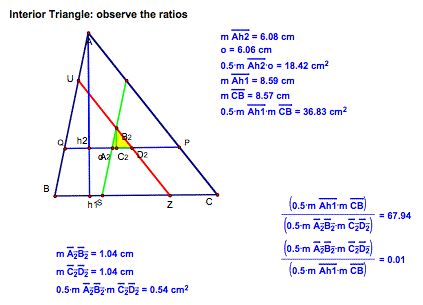
Notice when the triangle has all 3 bisecting lines there is a
small triangle formed in the interior of the triangle. Of course, we know that this triangle
is a similar triangle to the larger triangle but what would we expect to find in
the ratios of their areas?
Area of the interior = .0144
Area of the larger triangle
(note: GSP rounds to .01)
Is
this what you expected?
The information about the interior triangle did not provide as
much information I would have liked so it may be important to look
further.
B.
What is the ratio of the larger triangle to the new smaller triangle?
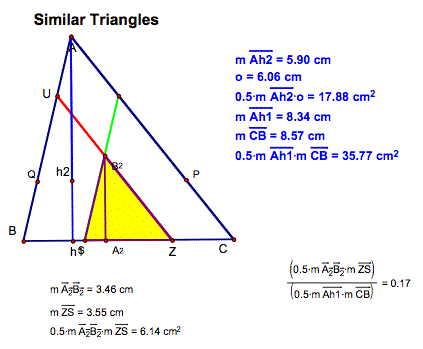
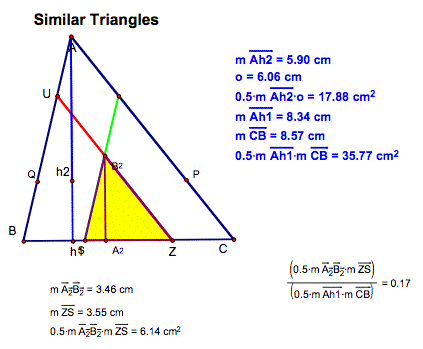
Notice when the triangle has all 2 bisecting lines there is a
similar triangle that is formed.
The areas of each of the two similar triangles are compared to the
larger triangle.
Area of smaller triangle = .1714
Area of the larger triangle
(note: GSP rounds to .17)
This area is greater than 1/6 and less than 1/5.
I would have imaged that this area would
be about 1/6th of the triangle.
B-2.
Should we take a look at the three triangles in relationship to each
other?
Notice that these three triangles are all similar to each other. Of course at this point one could then
compare all the sides with each other.
The following shows the three triangles and their respective ratios for
comparison.
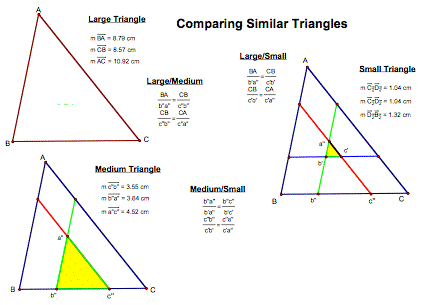
It is interesting to view these three triangles in relationship to each
other. If you go to the GSP
drawing you can observe that they change relative to their external triangles.
C. Prove that the measure of the three shaded areas in
each of the figures below are the same.
In each figure what is the ratio of the area of one of the regions to
the area of the original triangle?
What
is the ratio of the area of the three shaded areas to the original
triangle? 3trapezoids.gsp
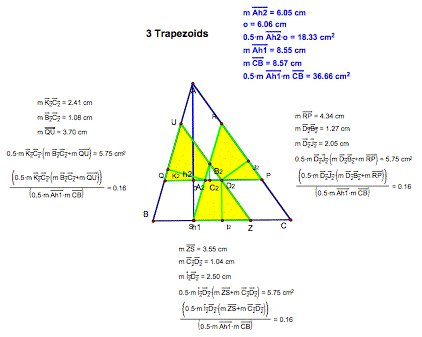
Notice when the triangle has all 3 bisecting lines (as before)
there are 3 trapezoids formed. The
areas of each of the trapezoids are equal and are compared to the larger
triangle.
Area of one trapezoid = .1566
Area of the larger triangle
(note: GSP rounds to .16)
If
all three trapezoids are combined there areas = .4698
(note: GSP rounds to .48).
This
is almost half the triangle. That makes sense!
What is the ratio of the area of the three shaded
parallelograms to the original triangle?
3parall.gsp
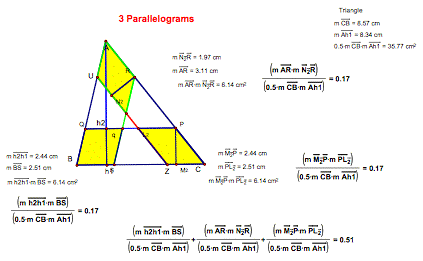
Area of one parallelogram = .1714
Area of the larger triangle
(note: GSP rounds to .17)
If
all three trapezoids are combined there areas = .5142
(note: GSP rounds to .51).
This
is a bit more than half the triangle.
That makes sense, as well!
The
only missing piece is the little triangle in the middle. All in all it would be safe to assume
that the 3 trapezoids areas together are a little less than the 3
parallelograms areas together.
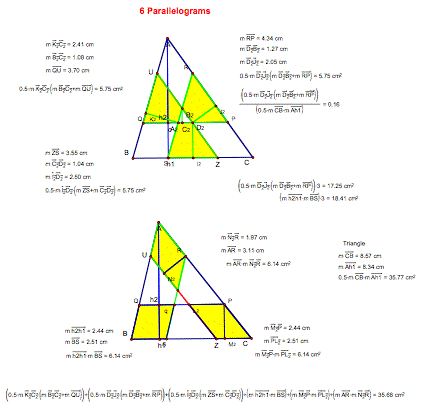
Take a look at the 6 parallelograms
Conclusion (maybe)?
It might be safe to say that there are many more comparisons that
can be done with the triangle.
Bisecting the area and comparing similar triangles only leads to other
comparisons that can be done. What
about the midpoints of each of the compared triangles? What about the Euler
lines; and so on. What happens
when the triangle is obtuse? Can these same comparisons be done?
So it is my belief that this investigation
can be and should be continued beyond the similar triangles that have been
revealed. This also lends itself
to a great project that can be and should be investigated in the classroom.
It is
said that
Curiosity
Killed the Cat!
Yes but

Satisfaction
Brought Her Back!