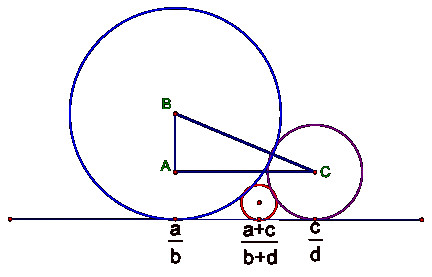
FordŐs Touching Circles
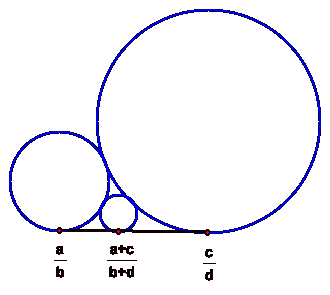
For the pictorial
presentation we begin with a straight line that can be considered the x-axis in
the plane. For any rational number
, a
circle tangent to that point with a diameter 
can be drawn. Some circles are tangent and others are not.
As discovered by Lester
R. Ford, if two circles corresponding to fractions 
and 
touch, then the circle corresponding to
the mediant fraction, 
, is
tangent to them both.
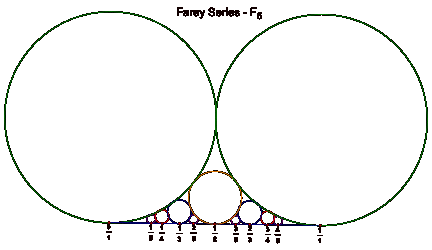
Recall, in the Farey
Series, the middle of any three successive terms is the mediant of the other two.
Therefore, the Farey Series 
can be interpreted geometrically using FordŐs Touching Circles.
To prove this idea that
if two circle corresponding to fractions 
and 
touch, then the circle corresponding to
the mediant fraction 
is tangent to both of them we need the
following theorem.
|
The two circles corresponding to |
For a complete proof
several cases of the relationship between the integers involved must be
considered. We will consider the
following case where b<d and 
< 
.
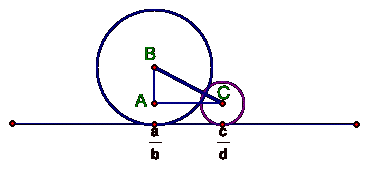
By construction,
when plugging the above
determined values for AB, BC and AC into the Pythagorean Theorem it directly follows that
Thus it follows that the two circles are tangent.
From 
, we can say 
and 
, thus
the mediant circle touches the other two if and
only if they are tangent to each other.
