The GOLDEN SECTION or PHI - Lesson
Introduction
I have seen it called the Golden Section but it is better known as the Golden Ratio. It is represented by the Greek letter Phi (f). In my research I have also found reference to the Greek letter, Tau (t).
There are early references to Phi by Pythagoras, a Greek philosopher around 550 B.C. The Pythagoreans gave particular interest to the pentagon. Greek architects' plans for their most famous temples and buildings (such as the Parthenon) used the Golden Ratio throughout the structure. Greek letter phi (Φ) is used to represent the golden ratio; this was the initial letter of the Greek architect, Phidias, who evidently used the Golden Ratio in much of his sculptures.
Phi gave many mathematicians in the Middle Ages and the Renaissance much to ponder. Luca Pacioli wrote a book called De Divina Proportione (The Divine Proportion) in 1509. It contains drawings made by Leonardo da Vinci of the 5 Platonic solids. It was probably Leonardo (da Vinci) who first called it the sectio aurea (Latin for the golden section). More recently the book The Divine Proportion by Dan Brown, though written as a novel, brings the mystical nature of the ÔGolden RatioŐ and some intrigue into Leonardo da VinciŐs secret life into the plot of the book.
Definition of Phi
In order to define Phi, let us first look at its properties. When you square a number greater than one it gets larger; when you square a fraction (a number between zero and one) it gets smaller. However, when you square zero, 0, or one, 1, it remains the same.
|
Squares that are bigger |
Squares that are smaller |
|
22 is 4 |
1/2=0á5 and 0á52 is 0á25=1/4 |
|
32 is 9 |
1/5=0á2 and 0á22 is 0á04=1/25 |
|
102 is 100 |
1/10=0á1 and 0á12 is 0á01=1/100 |
Exactly what is Phi?
Given: ABC
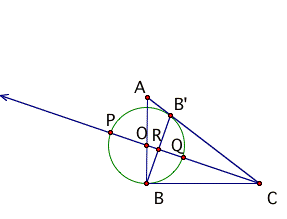
BC = 3.02 cm ABŐ = 1.99 cm PC/PQ = 1.62
BA = 4.00 cm CBŐ = 2.99 cm
AC = 4.98 cm PQ = 3.01 cm QC/OR = 1.63
QC = 1.85 cm
OR = 0.68 cm OR/RQ = 0.81
RQ = 0.83 cm
PC = 4.87 cm
(assume a 3, 4, 5 right triangle)
PC/PQ=f
PQ/QC = f
OR/RQ = f/2
Phi, Φ, = 1.61803
Now, we find Phi in our geometry as demonstrated, Phi is in music, and we find Phi in architecture.
Golden Rectanlge
As seen in the fun Disney movie, Donald in Mathmagic Land, the Golden Rectangle is used throughout history in architecture.
Golden Rectangle:
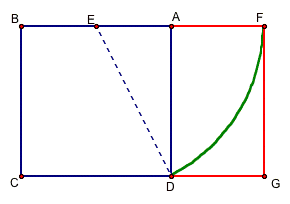
EB = 2.65 cm BF = 8.56 cm
EF = 5.92 cm FG = 5.29 cm
(EB+EF)/ FG = 1.62 BF/FG = 1.62
As the movie showed us, the Golden Rectangle is throughout the Parthenon at Athens. That structure was built in the 5th century B.C.E. This is not the only example. The Golden Rectangle is still used in architecture today.
The following is a construction of a regular pentagon.
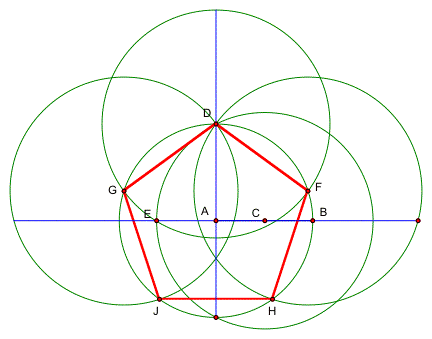
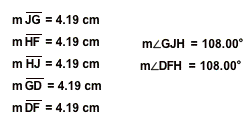
Now we remove the construction lines and add the diagonals.
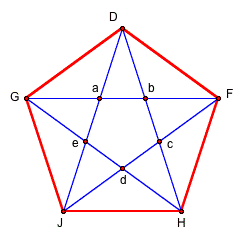
JF = 6.78 cm GF = 6.78 cm HD = 6.78 cm
Jc = 4.19 cm Gb = 4.19 cm Hd = 4.19 cm
JF/Jc = 1.62 GF/Gb = 1.62 HD/Hb = 1.62
GH = 6.78 cm JD = 6.78 cm
Gd = 4.19 cm Ja = 4.19 cm
GH/Gd = 1.62 JD/Ja = 4.19
These are not the only examples of Phi.
JUST for FUN:
¬ Have two students work together.
¬ Have one student measure the length of another studentŐs arm from the shoulder to the end of the middle finger.
¬ Now measure from the elbow to the end of the middle finger.
¬ Divide the larger number by the smaller number.
What do you get?
Can you calculate Phi to 10 digits? How about 20 digits? 100?
Here is the decimal value of Phi to 200 places grouped in blocks of 5 decimal digits.
The value of phi is the same but begins with
0á6.. instead of 1á6.. .
Read this as ordinary text, in lines across, so Phi is 1á61803398874...)
Digits:1á61803 39887 49894 84820 45868 34365 63811 77203 09179 80576 50 28621 35448 62270 52604 62818 90244 97072 07204 18939 11374 100 84754 08807 53868 91752 12663 38622 23536 93179 31800 60766 72635 44333 89086 59593 95829 05638 32266 13199 28290 26788 200
_____________________________________________________________
Conclusion
I am intrigued by PHI. The intent of this lesson and perhaps other future lessons with PHI is to open the eyes of young enthusiastic mathematic students to what may be beyond to ÔnormalŐ math lesson. Since PHI is used in so many different areas, it would be fun to discover other ways to investigate PHI. The students seem to enjoy some of the hands on lessons, such as measuring their arms. They are not as precise as may be necessary but they had a good time doing the exercise and it is surprising how well they did with the exercise.
I would enjoy working through more evaluations in mathematics concerning PHI but perhaps at a higher level than Middle School.