Final Assignment

by

Shridevi kotta

Click here to read the problem.

This write up explores and then proves the required theorem. In this write up you will have geometrical illustrations to follow along with the story. If you are interested in accessing the GSP file to explore for various locations of a given point or for various shapes of the triangle, click here to access the GSP file.

A..

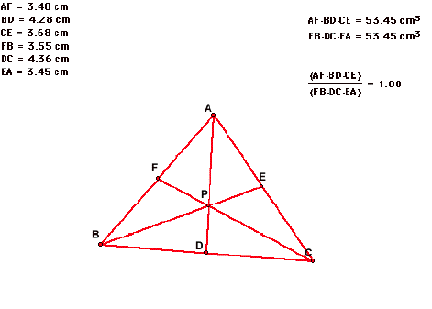
We are given a triangle ABC and when point P is inside the triangle. The ratios are as seen.

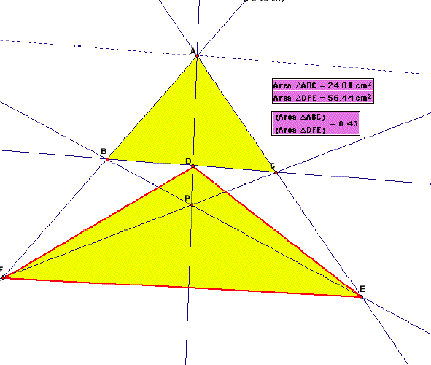
Moving the point to outside, we observe t he following.

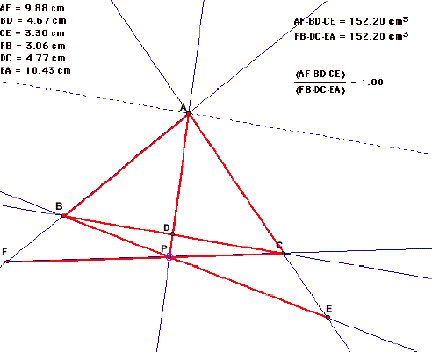
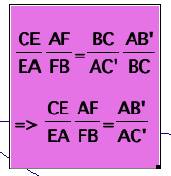
So, we observe by exploring for various locations of P or for various shapes of triangle ABC that, the (AF)(BD)(EC) = (FB)(DC)(EA) or that their ratio is 1.

B. Now the proof goes as follows.

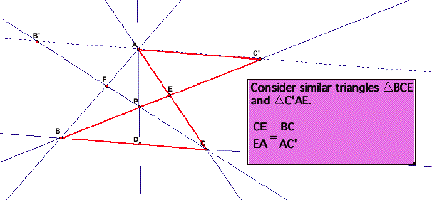
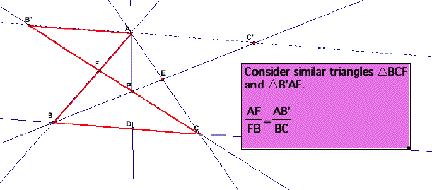
Hence we have,

Consider some more pairs of similar triangles.

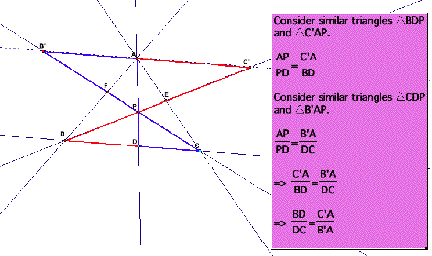
Hence

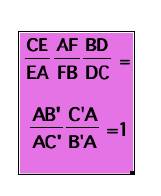
Thus proved the conjecture we made from exploration in part A..

C.

We see that as long as P is contained inside the triangle, DEF is bounded by the ABC and the ratio of ABC to DEF is 4 or greater than 4.

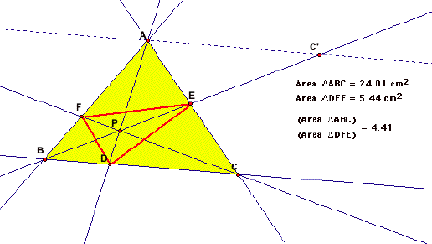
Just as an observation, if P is outside the triangle DEF can grow in size, and the ratio of triangle ABC to DEF can be smaller than 4.

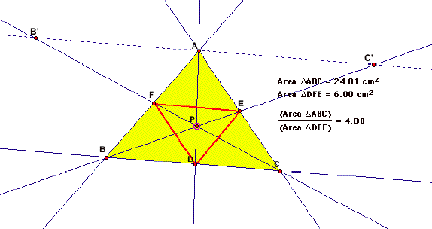
We observe that the ratio is equal to 4 when P coincides with centroid.

return