Assignment 11
by
Shridevi kotta
This write up explores polar equations using
graphing calculator software.
Here we investigate r = a +
b cos(kq) and explores for different
values of a, b and k and also compares with r = a + b sin(kq) and explains the observation made.
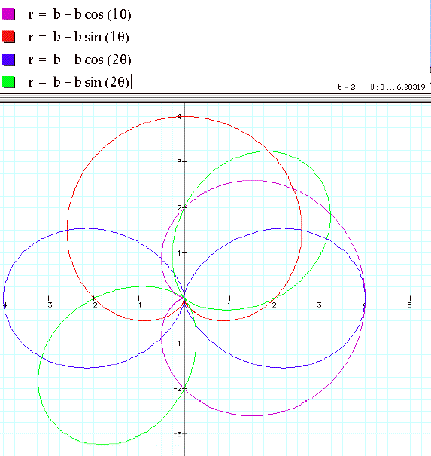
First lets look at r = a + b cos(kq), with a = b = 2(for any a
= b) and for different integer values of k.(we see that positive or negative
makes no difference, since cos(q) = cos(-q). For different integer
values of k, you get that many “k-leaf rose”, with leaves of magnitude b + b =
2b.
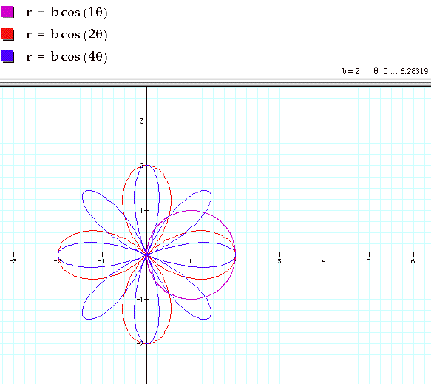
For the function, r = b cos(kq), we observe that the
leafs are of magnitude b.
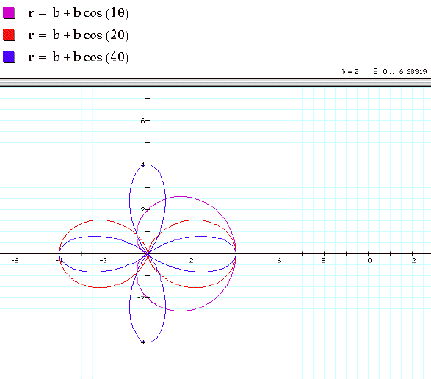
Consider the function r = a + b sin((kq) with a = b and k being
an integer values.
We observe that the function results in a “k-leaf
rose” with the difference from the cosine function being a phase shift. And the
phase shift is 90o/k. For example, 2 leaf rose has phase shift of 45o.
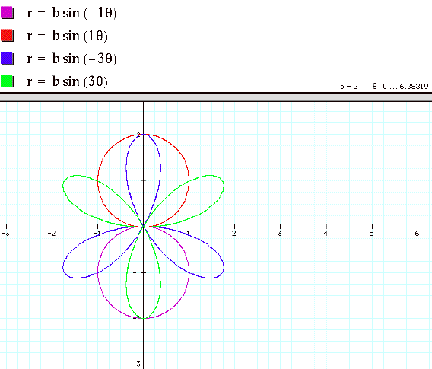
And in case of r = bsin(kq), if k is negative,
then the graph is flipped since
sin(-q) = -sin(q). Graphs are shown
below for comparison.