Assignment 3
by
Shridevi kotta
This write up explores graphs of quadratic
equation in different planes.
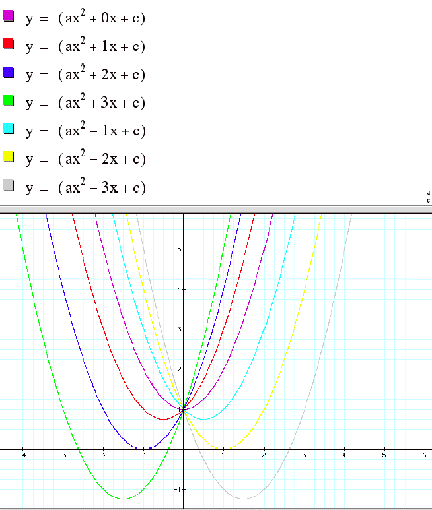
The general form of a quadratic equation
is y = ax2+bx+c. If we plot graphs
For
different values of b with a =c=1, graphs look as below.
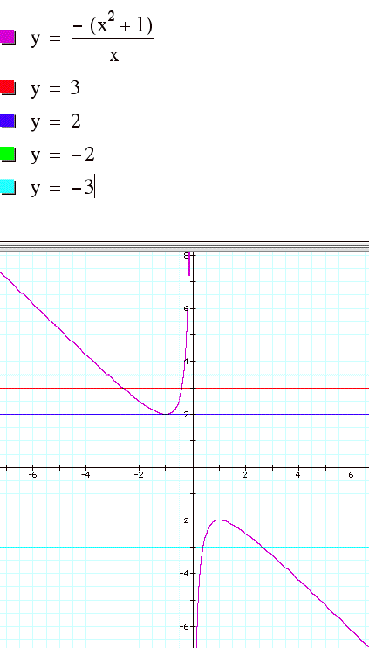
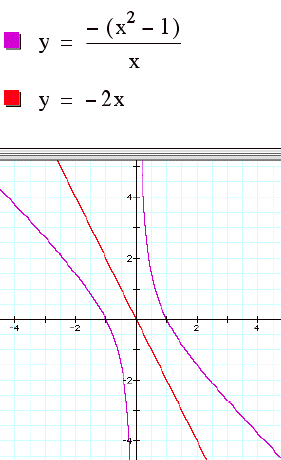
Let us consider the equation 0 = x2+bx+1. The
graph of this xb plane is obtained by solving for b. b = (- x2 Š1)/x.
When plotted in graphing calculator, your y is b.
If we take any particular value
of b, say b = 3, and overlay this equation on the graph we add a line parallel
to the x-axis. If it intersects the curve in the xb plane the intersection
points correspond to the roots of the original equation for that value of b. We
have the following graph.
For each value of b we select, we
get a horizontal line. It is clear on a single graph that we get two negative
real roots of the original equation when b > 2, one negative real root when
b = 2, no real roots for -2 < b < 2, One positive real root when b = -2,
and two positive real roots when b < -2.
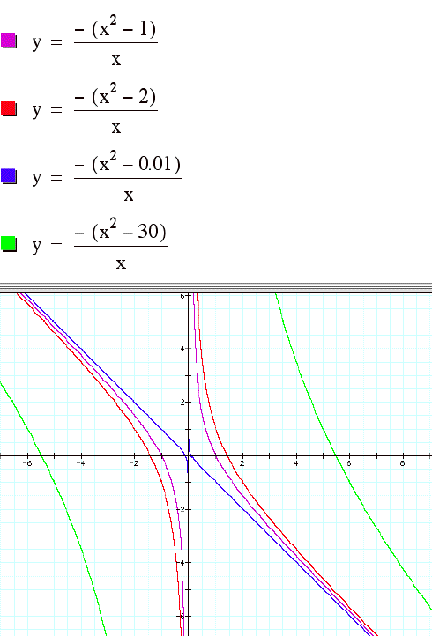
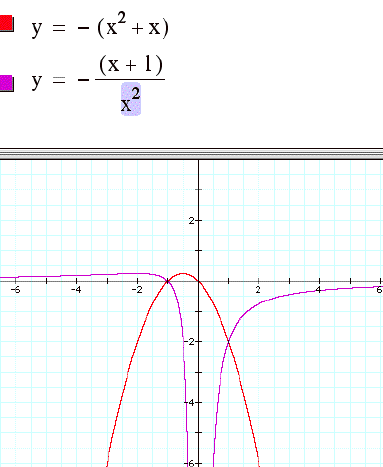
Moving along, if c = -1, -2 and so on Š30 and for c approaching 0, the graph looks
as follows:
For c = 0, the graph would be that of 2x+b = 0
which is a line as seen below.
The graph of 0 = x2+x+c in the xc
plane and 0 = ax2+x+1 in xa plane are as below:
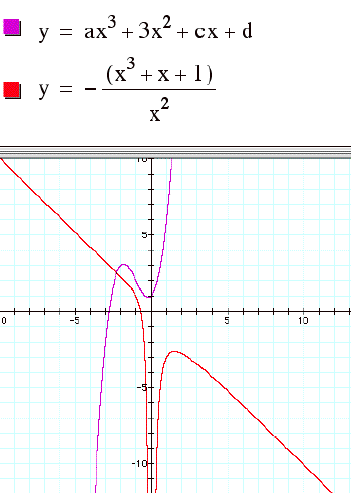
And now lets looks at the cubic equations. The
general form is y = ax3+bx2+cx+d.
If we plot graphs for different values of b with a =c=1, graphs look as below.
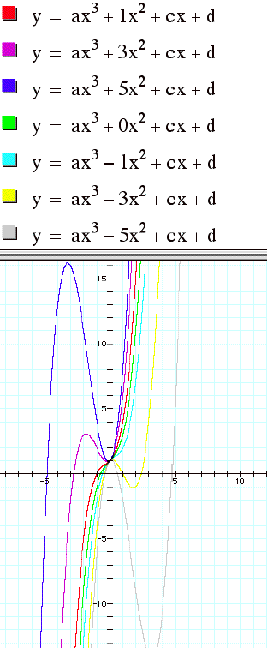
LetÕs consider the equation 0 = x3+bx2+x+1.
In the xb plane the graph look like the
following.