
Assignment 4
by
Shridevi kotta
This write up explores and proves some facts
about the centers of a triangle. In this write up you will have geometrical
illustrations to follow along with the story. If you are interested in accessing
the GSP file to explore the location of the center for various shapes of the
triangle, click on the highlighted word corresponding to that center to
download the file.
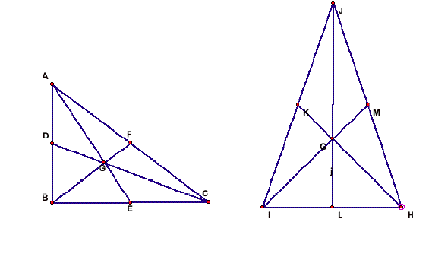
In any given triangle, the segment joining a
vertex of a triangle and the mid-point of the opposite side is called a median
of the triangle. Hence a triangle has 3 medians. And the three medians of a
triangle are concurrent. And the point of concurrency usually designated using
the letter G is called the Centroid
of the triangle.
In order to find the centroid of a triangle, it
is sufficient to find out the point of intersection of any two of the three
medians of a given triangle.
The third median has to pass through this point of intersection.
The perpendicular drawn from a vertex to the
opposite side of a triangle is called an altitude of the triangle. Again,
triangle has 3 altitudes. And the point of concurrency of the three altitudes
usually designated by letter H is called the orthocenter of a triangle. The
orthocenter of a triangle may lie in the interior of or on or in the exterior
of the triangle depending on whether the triangle is acute-angled, right angled
or obtuse angled respectively as seen below.
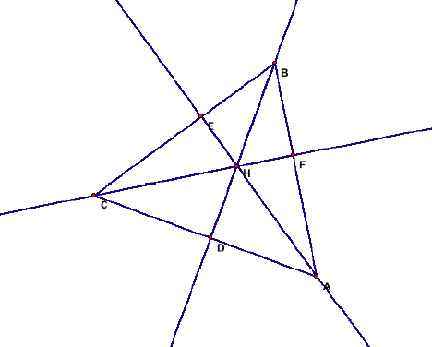
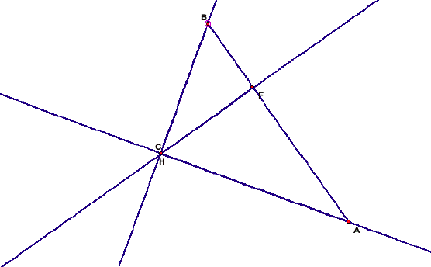
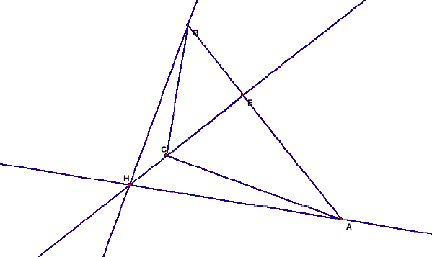
Again, in order to find the orthocenter of a
triangle, it is sufficient to find out the point of intersection of any two of
the three altitudes of that triangle.
The point of concurrency of the three angle
bisectors of a triangle is called the incenter
of the triangle. The letter used to designate incenter is usually I. By the
property of the angle bisector, the lengths of the perpendiculars from incenter
on the three sides will be equal. And if a circle is drawn with I as center and
the length of perpendicular as radius, it touches the sides of the triangle.
This circle is called incircle. Once again, in order to find the incenter of a
triangle, it is sufficient to find the point of intersection of any two angle bisectors of the
triangle.
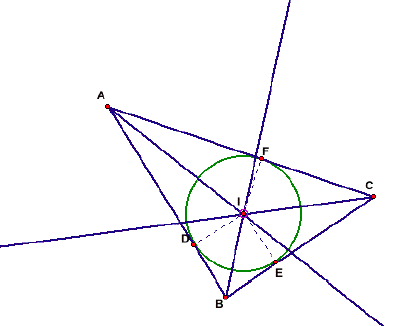
The perpendicular bisectors of the sides of a
triangle are concurrent and this point is called the circumcenter of a
triangle. The letter used to designate is C. Again, it is sufficient to find
the point of intersection of perpendicular bisectors of the triangle to find
the orthocenter. And by the property of perpendicular bisectors of the sides of
triangle, the point C is equidistant from the three vertices of the triangle.
The circle drawn with center as C and radius equal to the distance between C
and one of the vertices, the circle passes through the three vertices of the
triangle. This circle is called circumcircle. The circumcenter need not lie
within the triangle. It may lie in the interior of or on or in the exterior of
the triangle depending on whether the triangle is acute-angled, right angled or
obtuse angled respectively as seen below.
Lets now look at the proof of the theorem that
says , the three medians of a triangle are concurrent and the point of
concurrence , the centroid is two thirds the distance from each vertex to the
opposite side on the corresponding median.
We are given a triangle ABC in which the medians
BE and CF intersect at G. AG is joined and produced to meet BC in D.
We need to show that
i)
BD
= DC
ii)
AG:
GD = BG: GE = CG: GF = 2:1
Lets start with some construction that helps
with our proof. Extend AD to K such that AG = AK. Join BK and CK.
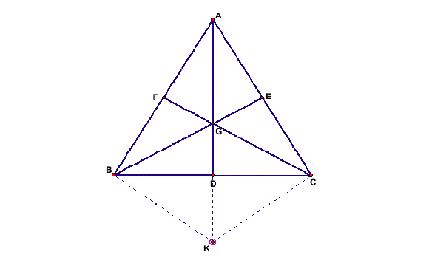
i)
In triangle ABK, given F is the midpoint of AB
and G is the midpoint of AK by construction.
Hence, FG || BK. And FG = 1/2 BC.
Similarly, if we consider triangle ACK, we see
that
GE || KC and GE = 1/2 KC.
In the quadrilateral BKCG,
BK || GC and KC || BG.
Hence, BKCG is a parallelogram.
BC and GK are the diagonals of the parallelogram
BKCG and intersect at D. Since we know diagonals of a parallelogram bisect each
other,
BD = DC!! Hence AD is the median from A.
ii)
We have,
GK = DK = 1/2GK.
GK = AG by construction.
Hence GD = 1/2AG.
Hence AG: GD = 2:1
Similarly we can prove BG: GE = CG: GF = 2:1