
Assignment 6
by
Shridevi kotta
This write up explores and proves some facts
about relationship between any given triangle and triangle formed by the
medians of the given triangle.
Click here to open
the GSP file and explore the relationship between the given triangle and
triangle of its medians, the values such as angles, perimeter, area, ratio of
perimeters, ratio of area for different types of given triangle by dragging one
of the vertices of the triangle.
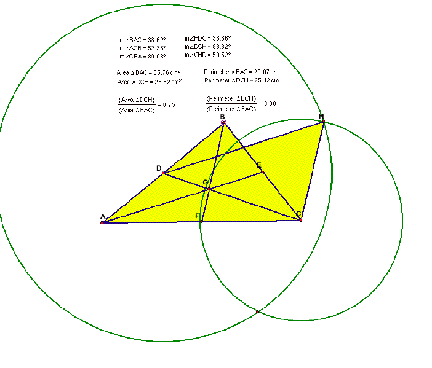
You observe through exploration, as you see in
the picture below that the triangles are neither congruent nor similar looking
at the angle measure. The perimeters or their ratios have no particular
relationship. When we do look at the ratio of area of the median triangle to
that of the given triangle, we notice that the ratio is a constant and equal to
0.75.
Lets try to prove this observation assuming some
of the known facts about medians and centroid (point of concurrency of medians
of a triangle) and area of a parallelogram. Click here
for GSP file or look at the picture below.
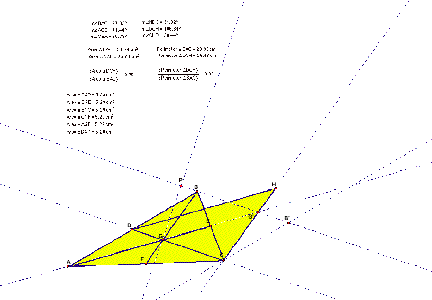
We know that AG = (2/3) AE and so on CG = (2/3) CD
and BG = (2/3)BF.
We also know that medians divide the triangle
such that the area of the divided triangles are equal (or half the original
triangle).
HereÕs the construction to help with our proof.
CGÕ is parallel to GB. DC is parallel to PBÕ and
GP is perpendicular to DC.
Consider the similar triangles CGGÕ and CDH.
We know CG = (2/3)CD. Hence by similar triangle
areas property,
Area of CGGÕ = (2/3 *2/3) area of median
triangle. = (4/9) area of median triangle.
But, from parallelogram, CGBGÕ, area of triangle
GBGÕ = (4/9) area of median triangle.
And also, that area of triangle BGE = area of
triangle EGC. Hence area of triangle GBC
= (4/9) area of median triangle----------------------(1***)
Similarly constructing some more parallel lines
we can prove that area of triangle EGC = area of triangle CGF = area of
triangle AGF = area of triangle DGA = area of triangle BGD.
Hence area of triangle GBC = (1/3) area of
triangle ABC -------------(2***)
From (1***) and (2***) we have
(4/9 ) area of median triangle = (1/3) area of
triangle ABC
The ratio, area of the median triangle /area of
triangle ABC = (3/4) = 0.75