
Assignment 9
by
Shridevi kotta
This write up explores some facts about Pedal
triangle. If triangle ABC is obtained by constructing lines through 3 points A,
B, C in a plane and P is a pedal point anywhere on the plane, then the pedal
triangle is constructed as follows:
Construct perpendicular lines from P to line
through AB intersecting at D. Similarly construct perpendicular through P to
line through BC intersecting at E and another perpendicular through P to line
through CA intersecting it at F. Triangle constructed by DEF is called the
pedal triangle for the pedal point P.
LetŐs first explore and see what happens to
pedal point if it is the centroid G of an equilateral triangle. The Pedal
triangle will be the medial triangle.
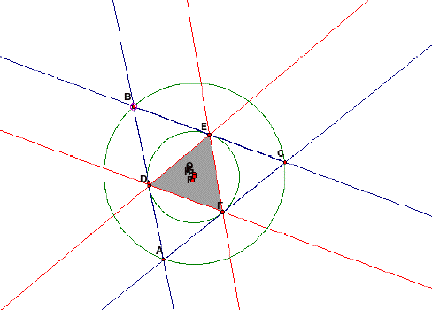
If the pedal point P is the Circumcenter O of ABC,
then the pedal triangle DEF is similar to the triangle ABC even when outside
ABC as seen below.

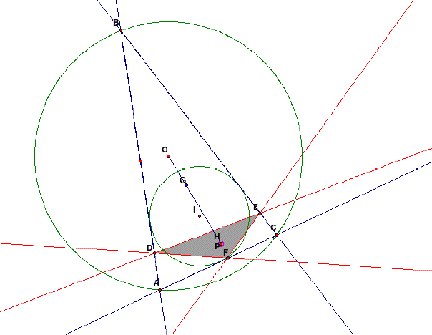
If P is H-orthocenter, then the pedal triangle
DEF is as below.
Click here to download
GSP file to do above explorations.
Now letŐs look at some more explorations as to
the locus of the midpoints of the pedal triangle when the locus of Pedal point
P a circle larger in radius than the circum-circle with the center being
circum-center. And when the circle is the circum-circle itself.
Click here for a GSP
file. Following are some of the observations.
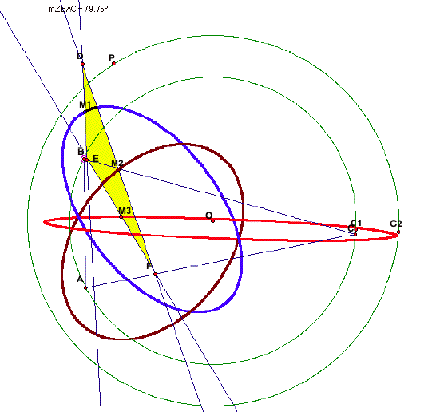
When the locus of P is on a circle larger than
the circum-circle, for an acute triangle, the loci of midpoints are ellipses.
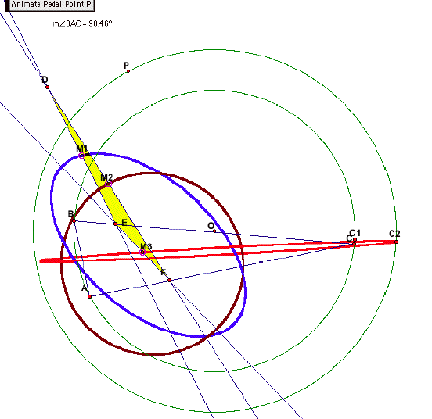
When the triangle ABC is a right triangle, the
loci of the midpoints are two ellipses and a circle.
And when the triangle is an obtuse, the loci of
midpoints is similar to the acute angled case with the fact that they form
ellipses.

When the locus of P is on the circum-circle, we
see that the pedal triangle is a degenerate triangle, with the vertices being
collinear and the line segment being called Simson Line.
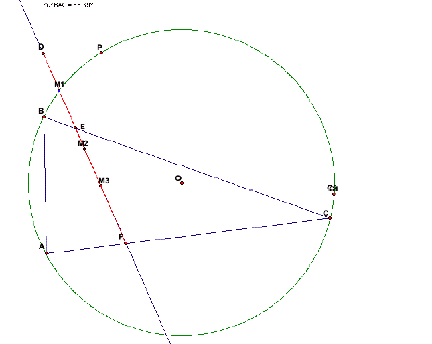
The loci of midpoints are the same as in the
above cases. When ABC is a right triangle, we notice that one vertex of pedal
triangle moves along the hypotenuse of the triangle ABC.
When P is at one of the vertices of ABC that is
not a right angle, two of the vertices of pedal triangle collapse to that point
with the third being at other vertex. When P is at the vertex with right angle,
two of the vertices of pedal triangle collapse to that point with the third
being on the hypotenuse at the intersection of perpendicular from opposite
vertex. This can be seen by dragging the pedal point P to vertices of ABC
triangle.