Assignment #1

By Amber Krug

---

Problem:

After graphing:

                           x2 + y2 = 1

                           x3 + y3 = 1

                           x4 + y4 = 1

                           x5 + y5 = 1

What is expected for the graphs of:

                           x24 + y24 = 1

                                or

                           x25 + y25 = 1?

---

First, let’s analyze the original graphs:

x² + y² = 1

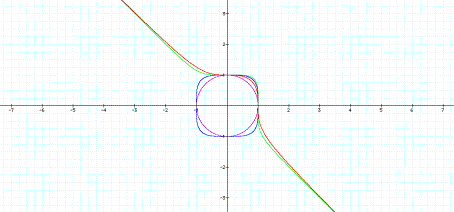
x³ + y³ = 1

x⁴ + y⁴ = 1

x⁵ + y⁵ = 1

The graphs begin to show that as the exponents of x and y increase the curves centered about the origin begin to develop into right angles.  The original circle begins to develop into a square as the exponents increase in even numbers.  See the graph below of increasing even exponents:

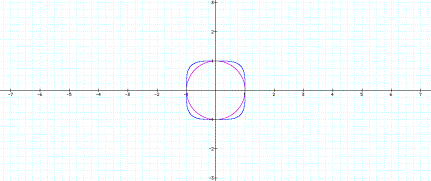
x² + y² = 1

x⁴ + y⁴ = 1

As the exponents increase in odd numbers, the original circular break in the line y = -x becomes more square.  See the graph below of increasing odd exponents:

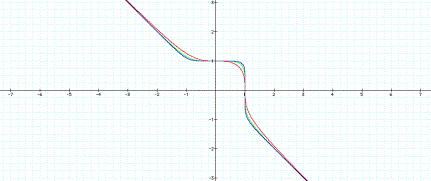
x³ + y³ = 1

x⁵ + y⁵ = 1

x⁷ + y⁷ = 1

According to these observations, the graph of

                           x²⁴ + y²⁴ = 1

should resemble a square, and the graph of

                           x²⁵ + y²⁵ = 1

should have a break resembling half of a square in the line y = -x.  Below is our predicted graph:

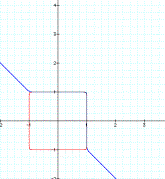
x²⁴+y²⁴ = 1

x²⁵+y²⁵ = 1

Return