Assignment
2:
Analysis
of y = ax2 + bx + c
Presented
by:
Amber Krug
y = ax2
+ bx + c
Using the above equation, the problem asks to fix two of
the values for a, b, and c and construct 5 graphs on the same axes as the third
value varies.
LetŐs start
by keeping a and b constant and vary c:
Below is the
graph of
y = x2 + x + c
where c = -8, -4, 0, 4, 8
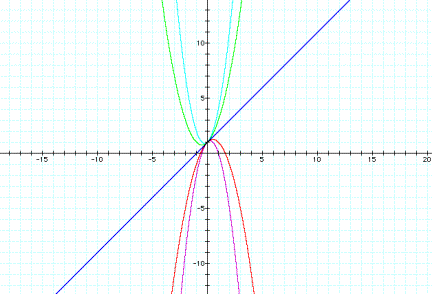
From the graph, we see that the x-value of the vertex
remains constant; however, the y-value of the vertex corresponds to the
c-value.
Notice the
shape and direction of each graph are the same.
Now, letŐs
keep a and c constant and alter b:
Below is the
graph of
y = x2 + bx + 1
where b = -6, -3, 0, 3, 6
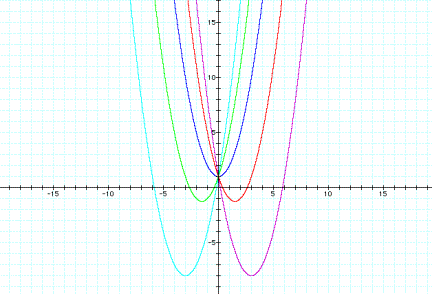
From the
graph, we see that the x-value and y-value of the vertex change, but the shape
and direction of each parabola is the same.
Lastly,
letŐs keep b and c constant and alter a:
Below is the
graph of
y = ax2 + x + 1
where a = -2, -1, 0, 1, 2
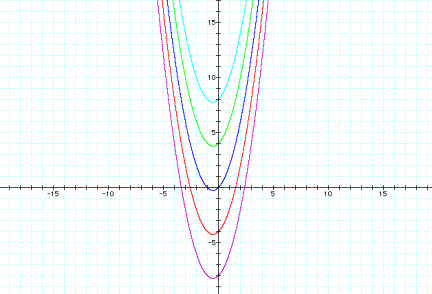
a controls
the direction of the graph. When a is negative, the graph opens to the
bottom, and when a is positive, the graph opens upward. The shape of the
graph changes with a as well.