Assignment #4:
Investigation of the
Circumcenter of a Triangle
By Amber Krug
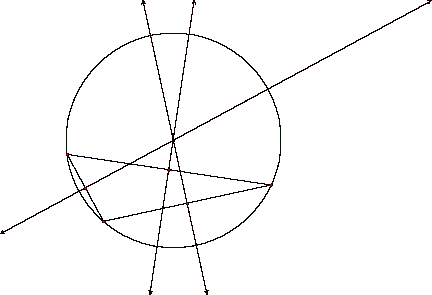
Our goal is to analyze the
circumcenter of a triangle. The
circumcenter of a triangle is the point in the plane equidistant from the three
vertices of the triangle.
We begin with a random triangle.

We then find the perpendicular
bisector of each side of the triangle.
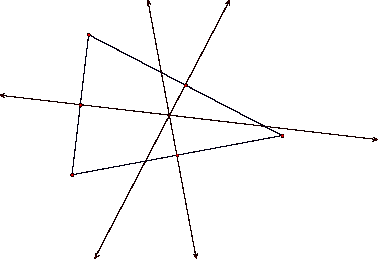
The point of intersection of
these three lines is the circumcenter of the triangle, which is more easily
seen by looking at the center of the circumcircle.

Now that we know what a
circumcenter is, letŐs look at the circumcenter for different triangles. LetŐs start with a right triangle.
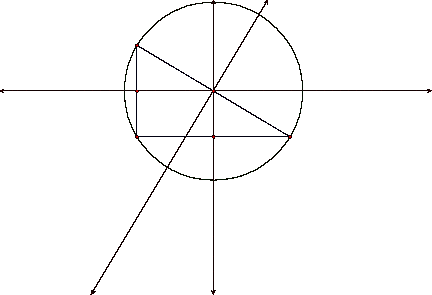
From the above illustration we
see that the circumcenter lies on the hypotenuse.
When we find the circumcenter of
an acute triangle we see that it lies inside the triangle (image A); however,
the circumcenter of an obtuse triangle lies outside the triangle (image B).
Image A
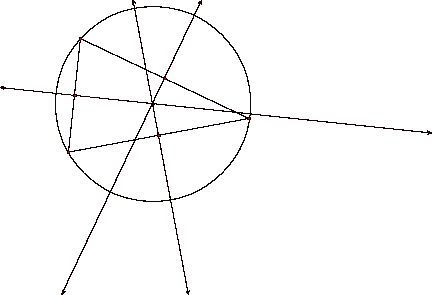
Image B