Assignment #7:
Tangent Circles
By Amber Krug
Given two circles and a point on one of the circles,
we can construct a circle tangent to the two circles with one point of tangency
being the designated point.
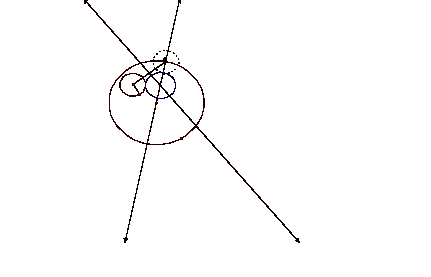
This
is accomplished by constructing a line between A, the given point, and the
center of the first circle. Then,
a circle with the same radius as the smaller circle is created with center
A. We then draw a line from A to
the center of the smaller circle.
The intersection of the perpendicular line to this segment at the
midpoint of the segment and the line through the center of the larger circle
and A is the center of our tangent circle.
I
experimented with the placement of A on the larger circle, and I found it
interesting that as A approaches the smaller circle, the tangent circle
decreases in size, and in fact, the tangent circle is constructed inside the
smaller circle. To see an
animation of this, click
here and hit the “Animate Point” button.