Assignment #8:
Altitudes and Orthocenters
By Amber Krug
Below is the construction of:
1. Any triangle ABC;
2. Orthocenter H of triangle ABC;
3. Orthocenter A of triangle HBC;
4. Orthocenter C of triangle HAB; and
5. Orthocenter B of triangle HAC.

My conjecture is that A is
the Orthocenter of triangle HBC, B is the Orthocenter of triangle HAC, and C is
the Orthocenter of triangle HAB.
Proof:
By
construction: BC is perpendicular to AH, AB is perpendicular to CH, and AC is
perpendicular to BH; therefore, the Orthocenter of triangle HBC lies on the
lines AH, AB, and AC. This must
occur at the intersection of these three lines which is A. Thus, A is the orthocenter of triangle
HBC.
Similarly,
B is the Orthocenter of HAC, and C is the Orthocenter of triangle HAB.
We can then
construct the circumcircles of ABC, HAB, HAC, and HBC:
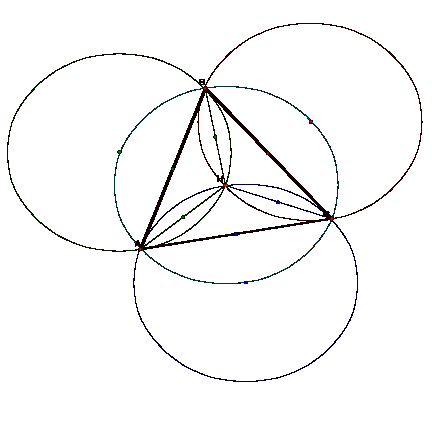
If we construct the
Nine Point Circles of triangles ABC, HAB, HAC, HBC, we find that the Nine Point
Circles are the same circle for each triangle.
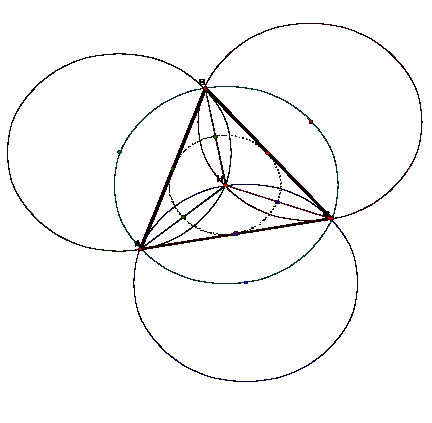
However, this is not
the case. This only occurs when
the Orthocenter H is in the center of the circumcircle of ABC.