Assignment #9:
Pedal Triangles
By Amber Krug
Let triangle ABC be any triangle. If P is any point in the plane, then
the triangle formed by constructing perpendiculars to the sides of ABC locate
three points R, S, and T that are the intersections. Triangle RST is the Pedal
Triangle for Pedal Point
P.
Below is an example
of a Pedal Triangle:
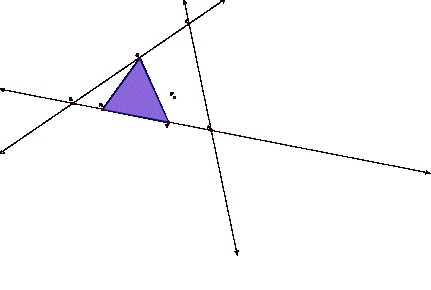
If the pedal point
is the orthocenter of ABC, then the one point of the pedal triangle is always
shared with one point on ABC even if the orthocenter is outside the triangle.
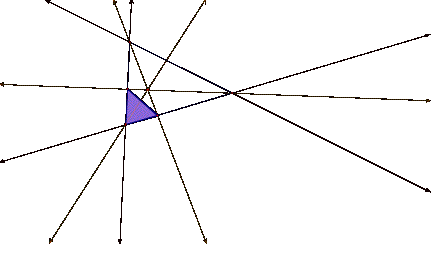
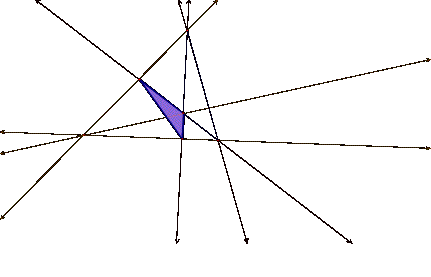
If the pedal point
is on one of the vertices of ABC, then one of three things can happen:
1.
The pedal triangle is
enlarged:
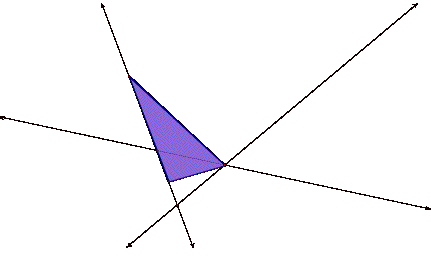
2.
The pedal triangle
becomes a line segment:
3.
The pedal triangle
becomes a point:
