By Na Young

6. Take any triangle. Construct a triangle connecting

the three midpoints of the sides. This is called the MEDIAL triangle.

It is similar to the original triangle and one-fourth of its area.

Construct G, H, C, and I for this new triangle.

Compare to G, H, C, and I in the original triangle.

By GSP, construct a triangle ABC and connect the three mid points of the sides,

then call the name of points P,Q,R .

This triangle PQR is called the MEDIAL triangle.

We will investigate this MEDIAL triangle. It is similar to the original triangle

and an area of the MEDIAL triangle is one-fourth of an original triangle.

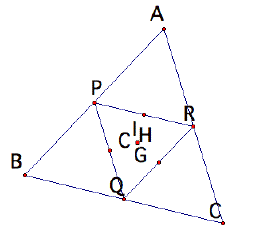
Construct G (CENTROID) of this MEDIAL triangle.

The CENTROID of a triangle PQR is made by constructing the three medians.

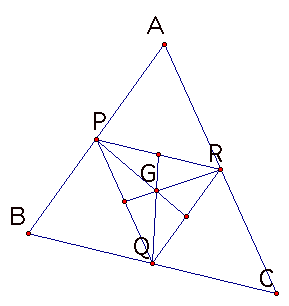
Next, construct H(ORTHOCENTER) of a triangle PQR.

It is the common intersection of the three lines containing the altitudes.

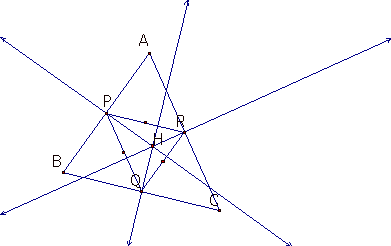
Construct C(CIRCUMCENTER) of a triangle PQR.

It is the point in the plane equidistant from the three vertices

of the triangle PQR.

We can make the CIRCUMCENTER of a triangle PQR

by the perpendicular

bisector of each side of the triangle.

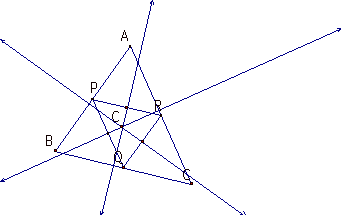
Next, construct I(INCENTER) of a triangle PQR.

We can make the INCENTER of a triangle PQR by the angle bisectors of

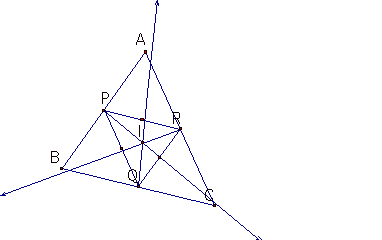
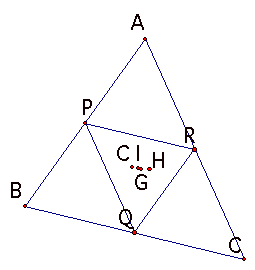
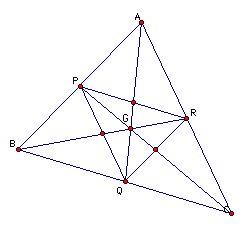
The following picture shows us C,G,H,I of a triangle PQR.

Compare these points to those of a original triangle. In the picture,

the red points C,I,G,H is the MEDIAL triangle’s ones and the white

blue points C’,I’,G’,H’ is the original’s ones.

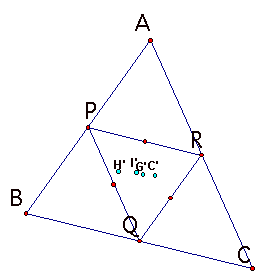
The points C’,G’,H’ are on the one line in the original triangle and C,G,H

of the MEDIAL triangle are also on one line.

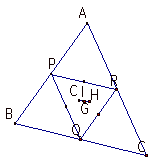
The CENTROID of a original triangle is always congruent to one of a MEDIAN triangle.

And the CENTROID is on the segment of the INCENTER of a original triangle

and I of a MEDIAN triangle.Moreover, it is on the segment between

the CIRCUMCENTER of a original triangle and one of a MEDIAN triangle

and also is on the segment between the ORTHOCENTER of a original triangle

and one of the MEDIAN triangle.

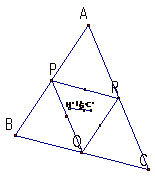
In the investigation of ORTHOCENTER, H of a MEDIAN triangle is congruent

to the CIRCUMCENTER of a original triangle and a mid point of H’

and H is the CIRCUMCENTER of a MEDIAN triangle.

The points of H, G, and C is always on the one line and hence, H, G, C, H’, G’

and C’ is on the one line because H, G, and C of a original triangle is on the one line

and H’,G’ and C’ is on the one line. In the case of regular triangle, all of G,C, H

and I is congruent.

………………………………………………………………………