Locus of a point
By Na Young
8. Of a triangle, given two vertices A and B, and the angle
at the third vertex C (the angle opposite side AB). What is the locus of the point C?
LetÕs investigate the special case.
Given two vertices A and B and assume the angle at the third vertex
C is a right angle. We know that a triangle which one side is a
diameter of the CIRCUMCIRCLE
has a right angle.
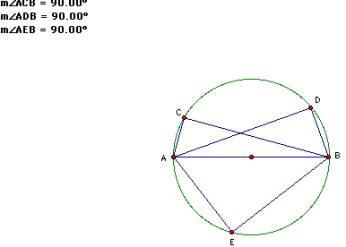
If any point on the circle is the third point, the angle at the third
vertex is 90 degrees. From this, we can think a similar situation.
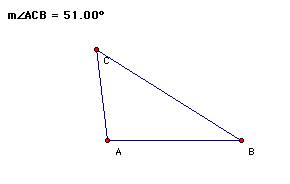
For
an example, make the angle at the third vertex C is 51 degrees.
Using GSP choose a mid point M of given
points A and B and draw
a perpendicular line from M. We draw
three perpendicular lines from
midpoints of three sides. Then we can
obtain a CIRCUMCENTER
of
a triangle ABC, We call the CIRCUMCENTER
O.
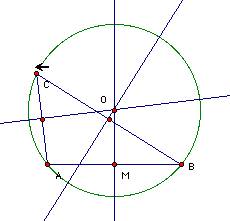
Now
we will investigate the change of an angle C.
Move
the point C on the circle O.
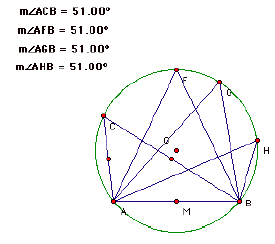
On the above circle of the
segment AB the angle C is not changed
and on the below of the segment AB the
angle C has a different
value of a given angle: That is, in
upper part of the segment AB
(containing a point C) the angle ABC is
always 51 degrees.
The locus of the point C is a part of
the CIRCUMCIRCLE of a
triangle ABC. Explicitly the locus is
an arc
ACB.
Another interest point is that the angle C is not changed on the
lower part of the segment AB.
Generally, we can say
when given two vertices A and B and the
angle at the third vertex C, the
locus of the point C is a part of the
CIRCUMCIRCLE of a triangle ABC:
Explicitly, an arc
ACB.
ÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉ
Return to Na
Young's Home Page