
Tangent Circles
By:† Lauren Lee
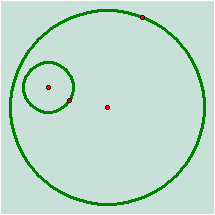
Given two circles and a point on one of the
circles. Construct a circle tangent to the two circles with one point of
tangency being the designated point.
To
construct a circle tangent to the two circles above, I used GSP.
The
construction is as follows:
First I
chose an arbitrary point on the large circle and construct a line that goes
through both the point and the center of the circle.
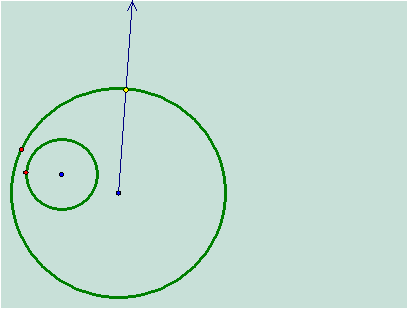
Next I
construct the radius of the small circle.†
I use this radius to form a new circle.†
My new circle is constructed using my arbitrary point as the center and
the radius of the small circle.† I also construct
a segment between the far intersection of the new circle and the line that goes
through the center of my large circle.
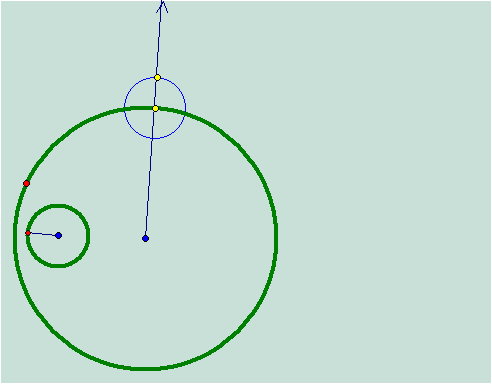
Next I
construct a segment from the midpoint of the small circle to the far point of
the new circle.† After I have done this,
I find the midpoint of the segment.†
Next I use the midpoint of the segment and the segment itself to
construct a perpendicular line.† My
perpendicular line intersects the line through the center of my circle.† This point of intersection is the center of
my tangent circle.
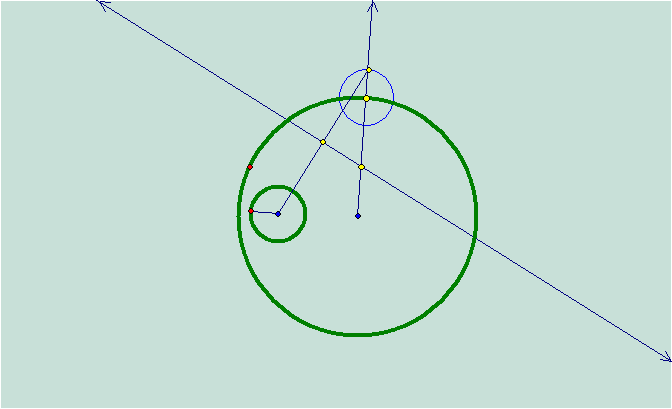
Now the
last step is to construct the tangent circle using its center and my arbitrary
point on the big circle.
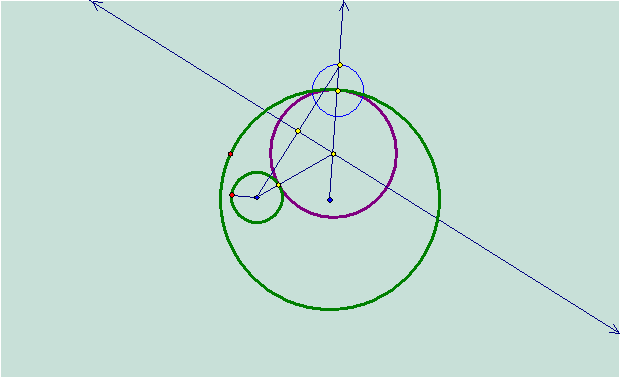
Now that
I know how to do the construction, I will investigate the locus of the tangent
circle.† With GSP, I trace the locus of
the tangent circle while my arbitrary point moves around the large green
circle.
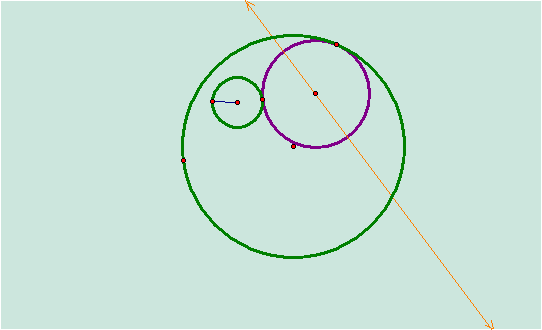
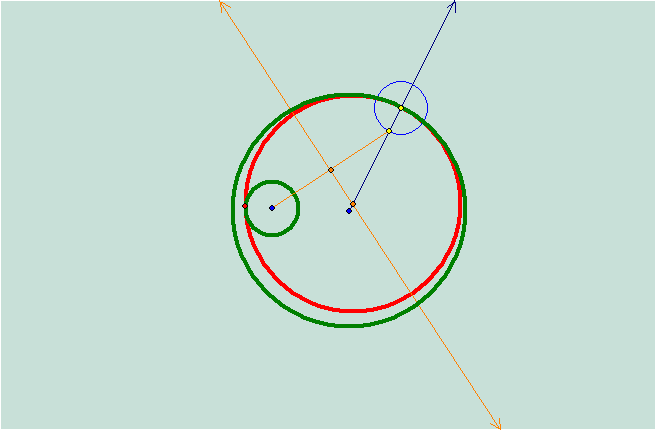
The red
circle is the traced line of the movement of the locus.† It appears to be an ellipse.† Notice that the orange perpendicular line is
tangent to the ellipse.† Will it always
be tangent as our arbitrary point moves around the circle?
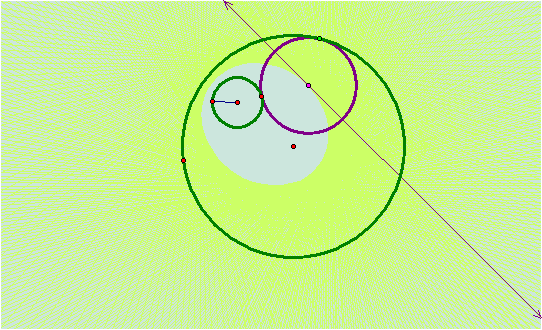
Yes, we
can see that the line will always be tangent to the ellipse.
Now letís
investigate a second tangent circle of the two green circles.
This
tangent circle will be constructed in a similar way.† The difference is that instead of constructing a segment from the
midpoint of the small green circle to the far point of intersection of the blue
circle and the line through the center, I will construct a segment to the lower
point of intersection of the blue circle and the center line.
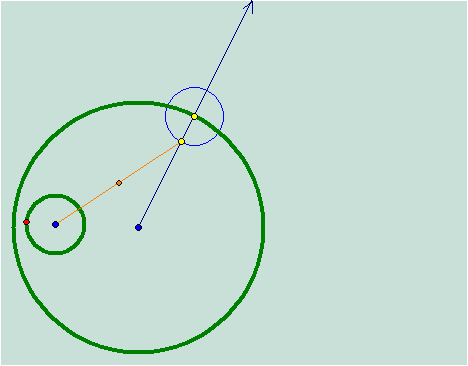
The rest
of the construction is the same, resulting in the following red tangent circle.
Now we
have a case where one of the green circles is inside of the tangent
circle.† Letís see what happens when we
trace the locus of the tangent circle.
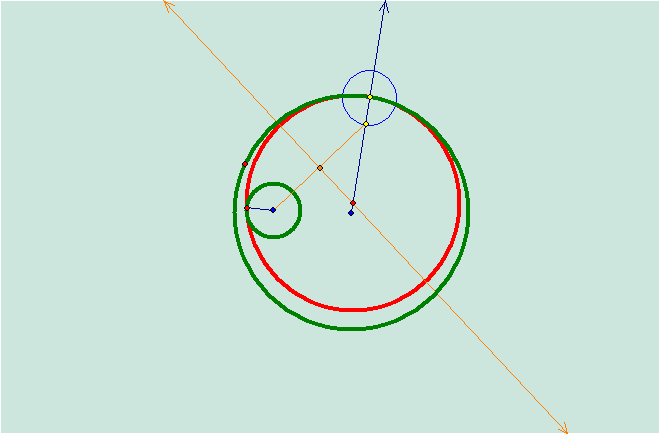
As you
can see, the locus of the tangent circle appears to form an ellipse.
Now letís
investigate the tangent circle of two intersecting circles
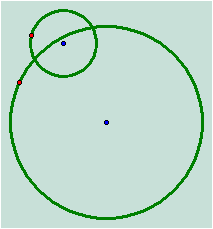
The
tangent circle is as follows:
What
about the locus of the tangent circle?
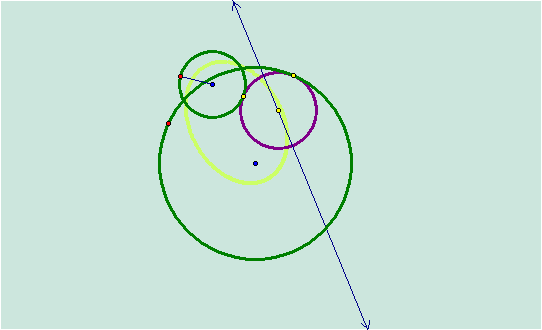
By
tracing the locus, we can see that the ellipse goes outside of the large
circle.
What
about the perpendicular line?† Will it
still always be perpendicular to the ellipse?†
YES!

Letís do
another investigation:
What
happens now if we change the construction as before to find the other tangent
circle?
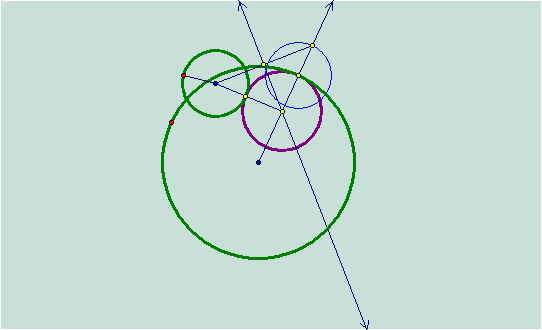
Letís
construct a segment from the midpoint of the small green circle to the lower
point of intersection of the blue circle to find the other tangent circle.
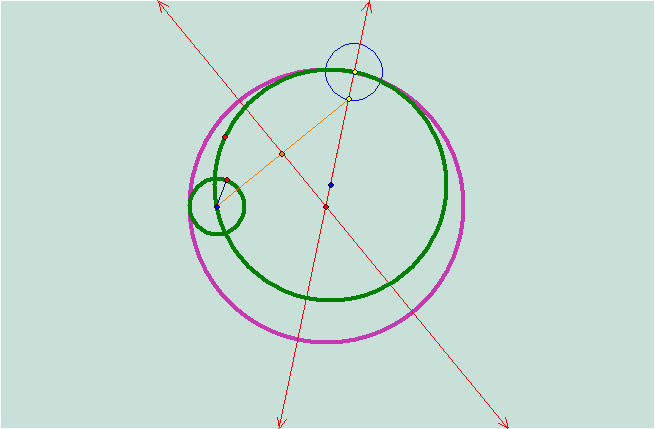
Now both
of the green intersecting circles are inside of the purple tangent circle.† What will happen with the locus of the
tangent circle?
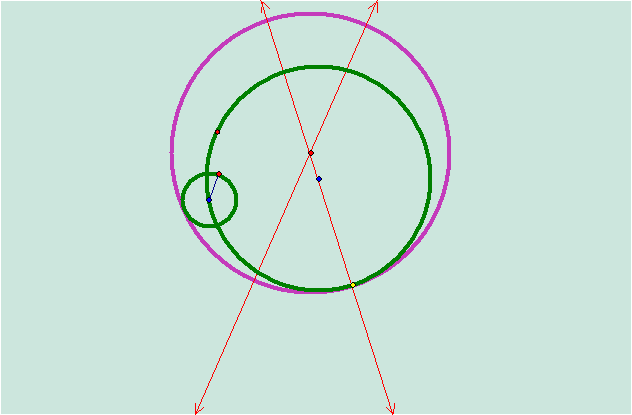
You can
see that the locus of the tangent circle has formed a hyperbola.† So what will happen when we trace the
perpendicular line?
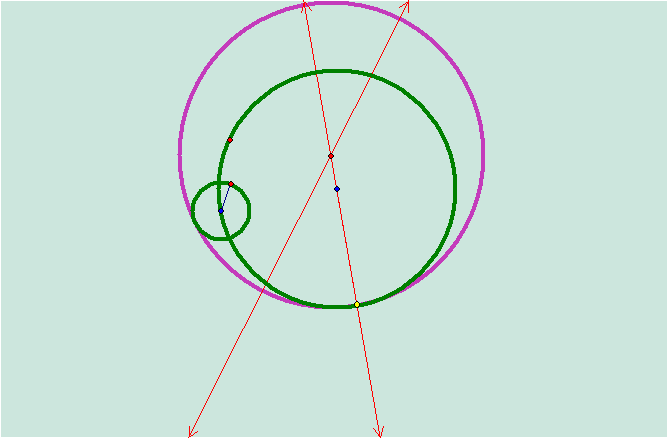
The
perpendicular line is still tangent to the locus of the tangent circle.
From
these investigations, we can see that the locus of the tangent circle does not
always form an ellipse.† Also, the
perpendicular line will always be tangent to the locus of the tangent circle.
If you
want to investigate further, here is my script tool for