________________________________________________________________________

Altitudes and Orthocenters

By: Lauren Lee

________________________________________________________________________

Problem:

1. Construct any triangle ABC.

2. Construct the Orthocenter H of triangle ABC.

3. Construct the Orthocenter of triangle HBC.

4. Construct the Orthocenter of triangle HAB.

5. Construct the Orthocenter of triangle HAC.

6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.

________________________________________________________________________

To setup this problem, I constructed a triangle using GSP. To construct the orthocenter of my triangle ABC, I must find the intersection of the altitudes of my triangle. I labeled the orthocenter H. Here is what I have at this point:

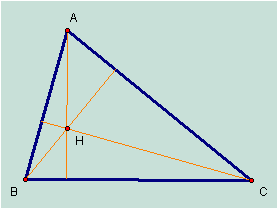
One thing that I observed from looking at my triangle is that I have created 6 triangles inside my large triangle. Also, in this particular triangle, the orthocenter lies inside, however that is not always the case.

My next step was to find the orthocenters of triangles HBC, HAB, and HAC.

Here is the orthocenter of triangle HBC:

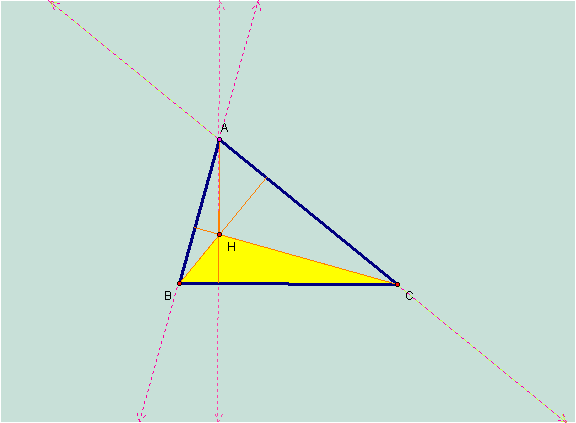
Here is the orthocenter of triangle HAB:

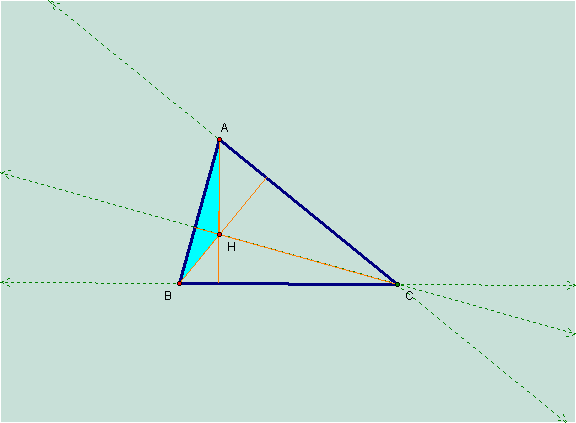
From your observations of the two triangles above, can you guess where the orthocenter of triangle HAC is? Let’s see if you’re right!

Orthocenter of HAC:

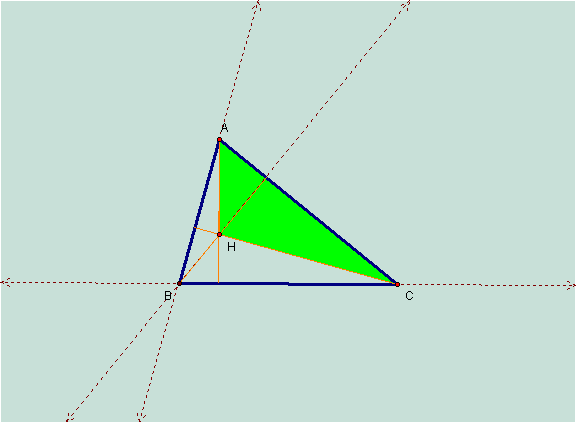
Now we can make a conjecture that the orthocenters of the orthic triangle lie on the vertices of the original triangle.

Now I am ready to construct the circumcircles of my triangles ABC, HAC, HBC, HAB. Before I can construct them I have to find the circumcenters of my triangles. Here is my construction:

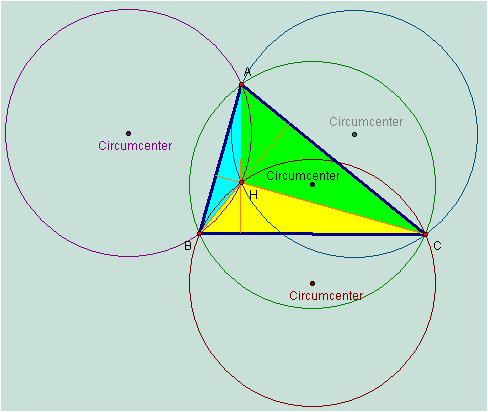
One thing that can be seen from my picture is that all of the circles go through point H, the orthocenter of triangle ABC. Also, all of the circles appear to be equal in size. Let’s try to prove this conjecture.

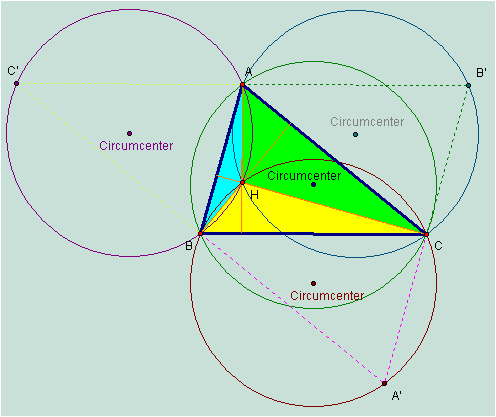
I have decided to translate the orthic triangle of ABC to triangles HBC, HAB, HAC. We now have a better picture of comparison. We can see, for example, in the bottom circumcircle, that AC = BA', and AB = A'C. So now we have shown that all of the circumcircles are of the same size!

Return