
Assignment 7
Tangent Circles
By
Ken Montgomery
In this study we wish to explore the
relationships between circles that are tangent and in particular the Locus of a
circle that is tangent to two other circles.
First we use two script tools (Outside
Tangent Circle, and Inside Tangent Circle), which can be downloaded
from Assignment 5, to construct
tangent circles. In the first investigation, we use the Outside Tangent
Circle tool to perform the construction in Figure 1.
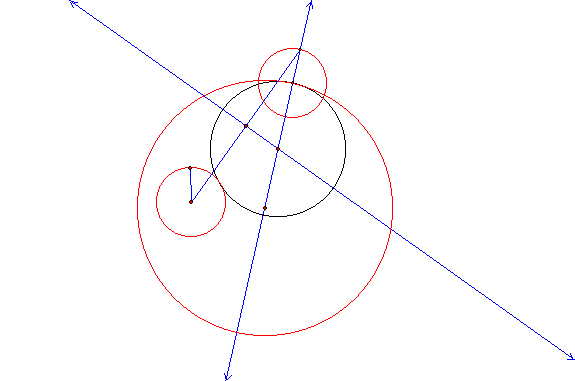
Figure 1: Black circle, tangent to
two red circles
In Figure 1, the black circle is tangent to the
two red circles. Here the tangent circle is inside a larger circle and outside
of the smaller circle. If the tangent circle is animated, such that it orbits
the small circle, while we trace its center, we obtain the locus in Figure 2.
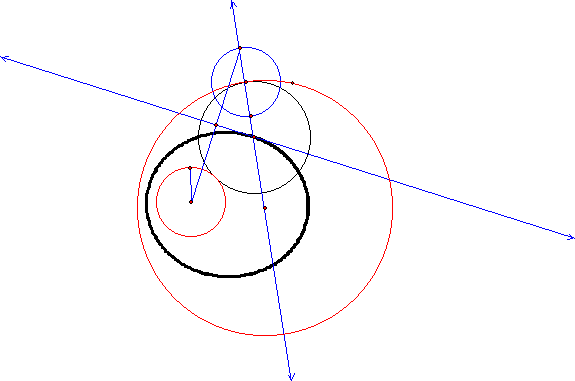
Figure 2: The locus of the black
(tangent) circle’s center
We label the center of the tangent circle, A,
the center of the big red circle B and the small red circle C. Next, we
construct segments
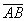 and
and
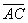 . We can see that as the circle rotates, the sum of
the two segments AB and AC is equal to the sum of the radii of the two red
circles (Figure 3).
. We can see that as the circle rotates, the sum of
the two segments AB and AC is equal to the sum of the radii of the two red
circles (Figure 3).
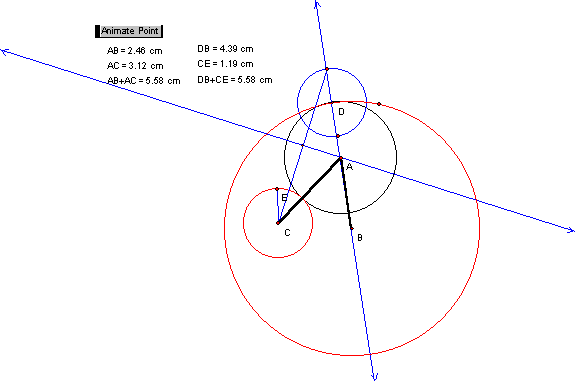
Figure 3: Comparison of circle radii
and center distances
The locus of the center of the tangent circle
is an ellipse, although this is not proven in general. Download OutsideCircle.gsp to explore this further.
In the second investigation, we use the Inside
Tangent Circle tool to perform the construction in Figure 4.
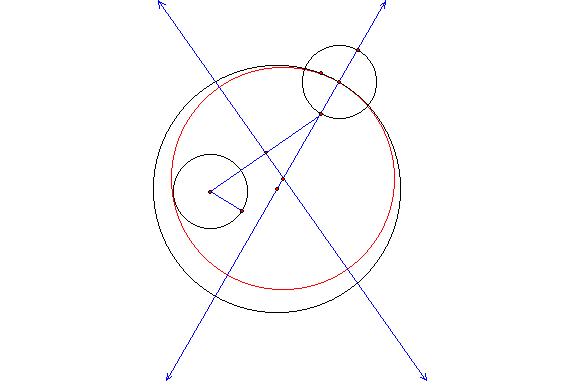
Figure 4: Red circle, tangent to two
black circles
In Figure 4, the red circle is tangent to the two
black circles. Here the tangent circle is inside a larger circle and containing
the smaller circle. If the tangent circle is animated, such that it orbits the
small circle, while we trace its center, we obtain the locus in Figure 5.
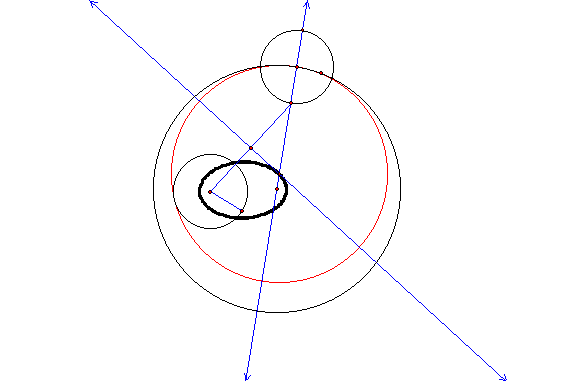
Figure 5: The locus of the red
(tangent) circle’s center
Again, we label the center of the tangent
circle, A, the center of the big black circle B and the small black circle C.
Next, we construct segments
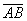 and
and
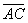 . We can see that as the circle rotates, the sum of
the two segments AB and AC is equal to the difference of the radii of the two
black circles (Figure 6).
. We can see that as the circle rotates, the sum of
the two segments AB and AC is equal to the difference of the radii of the two
black circles (Figure 6).
Figure 6: Comparison of circle radii
and center distances
The locus of the center of the tangent circle
is an ellipse, although this is not proven in general. Download InsideCircle.gsp to explore this further.
As an extension of the second investigation, if
the small black circle is moved outside of the large black circle, such that
the two are disjoint, but the red circle is still tangent to both of them, the
locus of the red (tangent) circle’s center is a hyperbola as demonstrated in
Figure 7.

Figure 7: Red circle tangent to
 and
and

Note that the difference between the segments
 and
and
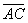 is equal to the difference between the two circle’s
radii,
is equal to the difference between the two circle’s
radii,
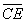 and
and
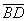 .
.
A similar extension is made of the first
investigation. If we move the small red circle outside of the large red circle,
such that the two are disjoint and still mutually tangent to the black circle,
we have the locus given in figure 8.
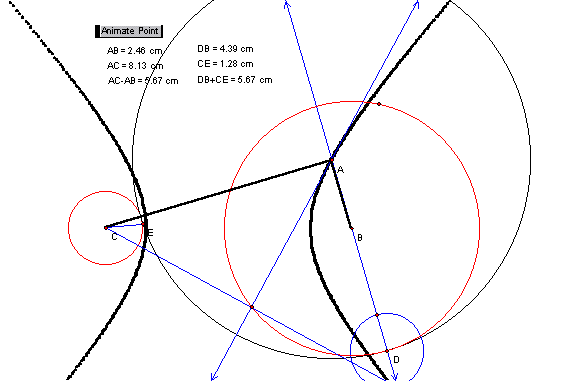
Figure 8: Black circle tangent to
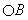 and
and
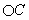
Note, again that the difference between the
segments
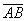 and
and
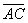 is equal to the difference between the two circle’s
radii,
is equal to the difference between the two circle’s
radii,
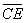 and
and
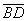 .
.
Return to Homepage



![]() and
and![]() . We can see that as the circle rotates, the sum of
the two segments AB and AC is equal to the sum of the radii of the two red
circles (Figure 3).
. We can see that as the circle rotates, the sum of
the two segments AB and AC is equal to the sum of the radii of the two red
circles (Figure 3). 


![]() and
and![]() . We can see that as the circle rotates, the sum of
the two segments AB and AC is equal to the difference of the radii of the two
black circles (Figure 6).
. We can see that as the circle rotates, the sum of
the two segments AB and AC is equal to the difference of the radii of the two
black circles (Figure 6). 

![]() and
and![]()
![]() and
and![]() is equal to the difference between the two circle’s
radii,
is equal to the difference between the two circle’s
radii,![]() and
and![]() .
. 
![]() and
and![]()
![]() and
and![]() is equal to the difference between the two circle’s
radii,
is equal to the difference between the two circle’s
radii,![]() and
and![]() .
.