Assignment 8

A Proof of Congruent Circumcircles

By

Ken Montgomery

Triangle ABC is constructed (Figure 1) using The Geometer’s Sketchpad©.

Figure 1: 

A tool for construction of the orthocenter (Assignment 5) is used to construct the orthocenter, H. Segments , , and are constructed in red (Figure 2).

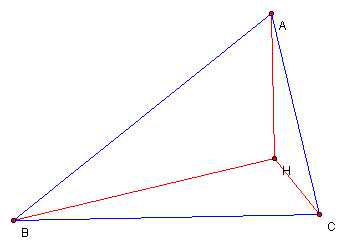
Figure 2:  with orthocenter, H

The circumcenter, O is constructed by a tool (Assignment 5), and given in Figure 3 with segments connecting it to the three vertices of the triangle.

Figure 3:  with orthocenter, H and circumcenter, O

The circumcircle for is then constructed in purple (Figure 4).

Figure 4:  with circumcircle in purple

We then use our tools to construct the circumcenter, O’ and circumcircle (red) of (Figure 5).

Figure 5:  with circumcenter, O’ and circumcircle in red

At this point we hypothesize that the circumcircles for , , and  are mutually congruent. We prove this as a theorem.

Theorem: The circumcircles for , , and  are congruent

Proof:

We first construct the segments,  and (Figure 6).

Figure 6: 

Now since AC is a shared side of  and  , then by definition, both circumcenters, O and O’ lie on the perpendicular bisector of AC (Figure 7).

Figure 7: O and O’ both lie on the perpendicular bisector of 

Quadrilateral COAO’ is formed by segments CO, OA, AO’ and O’C. The diagonals of the quadrilateral are AC and OO’. Since  , quadrilateral COAO’ is a rhombus and by definition we have . Since OA is the radius of the circumcircle for and O’A is the radius of circumcircle for  , the circumcircles are congruent and without loss of generality, the circumcircles for  , , and  are also congruent (Figure 8).Ò

Figure 8: The circumcircles for  , , and  are congruent

Download Assign08KM.gsp to explore this problem.

Return to Homepage