An Exploration of the Cycloid

By

Kenneth E. Montgomery

Description

For a wheel rolling along a line (Figure 1), we let the point of tangency for the circle and line be point T. The circle has center, C and radius . is the line segment congruent to the radius, k that is perpendicular to the line on which the circle is rolling, which we have taken to be the x-axis. is the line segment, parallel to the x-axis, formed by endpoints R and S, which is the segment’s intersection with . We then have the right triangle,, with . The locus of points formed by R, as the circle rolls along the x-axis is known as the cycloid and is given by the pink trace in Figure 1.

Open this GSP file to explore the cycloid of a circle, rolling along the x-axis.

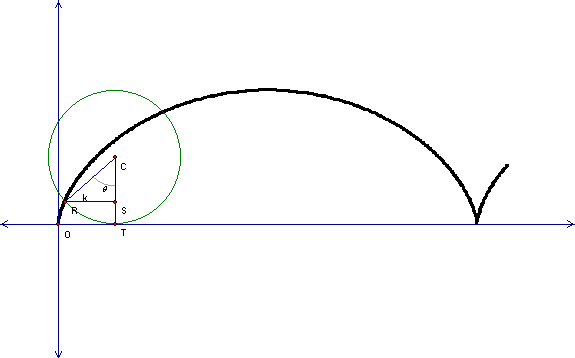
Figure 1: Cycloid of a wheel rolling along the x-axis

Derivation of Parametric Equations for the Cycloid
Let be the parameter. Then , since the circle is rolling along the x-axis. We have the center, C given by:

From , we have

Thus, we have

The parametric equations for the cycloid are therefore given by

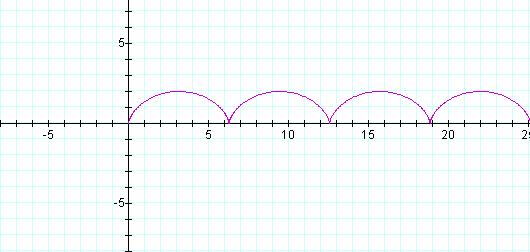
We then plot these parametric equations in Graphing Calculator 3.2 to obtain the graph in Figure 2, for four revolutions of the wheel.

Figure 2: , 

Open this GCF file to explore the cycloid in Graphing Calculator.

Return to Homepage