TAXICAB GEOMETRY

What is Taxicab Geometry?

What is this thing called Taxicab Geometry? What’s the difference between this type of geometry and the regular geometry we use in school? Let’s see….

Euclidean Geometry, known as Classical Geometry, is the normal everyday geometry we deal with in most of our classes. Here you have the familiar looking circles, ellipses, parabolas, etc. The shortest distance between two points is a straight line in Euclidean Geometry. This distance is found by taking the square root of the sum of the squares of the differences between x and y coordinates of the two points.

Non-Euclidean Geometry is a bit different. Our figures that we are so familiar with take on different shapes, and the distance between two points is found in a different way. When examining Taxicab Geometry, you are exploring one of the most simple forms of Non-Euclidean Geometry. In order to fully understand Euclidean Geometry, it helps to have some contact with this thing called Non-Euclidean Geometry.

Taxicab Geometry and Distance…

To begin with, let’s start with what we know. We know in Euclidean Geometry, we use the very familiar distance formula to find the distance between two points. This formula is the square root of (x₂ – x₁)² + (y₂ – y₁)². Now, in Taxicab Geometry, we cannot utilize this formula, because in Taxicab Geometry, you cannot go across blocks – you must count blocks in order to find distances. Take a look at this example…

Below is an example grid of streets in a city. All of the streets are parallel or perpendicular, and all city blocks are of equal size. John is at point A, and Bob is at point B. Distances are measured by counting the smallest number of city blocks it would take to travel from point A to point B.

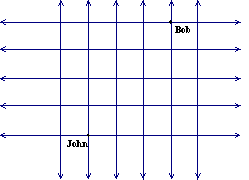
How many blocks does John walk to get to Bob? Is this the only route? Can John take more than one route to get to Bob?

John must walk a total of 6 blocks. There are several routes he can take to get there, but the quickest way, regardless of which route he takes, will be 7 blocks. Examine the various routes John can take to get to Bob:

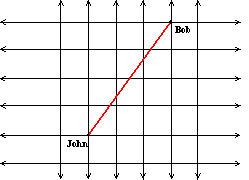
John could take even more routes, but the given routes are the shortest distances. If he felt like it, he could take a longer walk, and take more than 7 blocks. Now, let’s say John and Bob could cut across blocks – in other words, they are not limited to taking blocks – we are pretending there is open parkland. What is the shortest distance? What formula helps you derive this distance?

The shortest distance will be via the red line, utilizing the Pythagorean Theorem. This familiar theorem gives us a distance of = = 5. This is somewhat smaller than the answer we received in (a). Picture A shows the shortest route, and Picture B shows the triangle that is formed to get this distance.

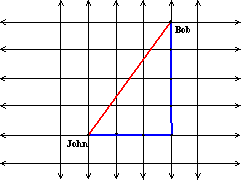
Picture A Picture B

So we see that we only come up with one shortest route when using the traditional distance formula, and it is quite smaller than the distance using Taxicab Geometry. In Taxicab geometry, there are several routes that can be taken, and several distances can be found.

So how can we come up with a simple formula for finding these Taxicab distances? Let’s see. If we let A and B be points on the Cartesian plane, how can we find a formula for Taxicab distances? Try playing around on graph paper to determine how you might find the formula. Eventually, you see the best formula to find the distance between two points in Taxicab Geometry is: |y₁ – y₂| + |x₁ – x₂|

Are there cases when Euclidean and Taxicab distances are the same? Yes there is! When the points lie on the same vertical or horizontal line, our distances will be the same, regardless of what formula we use.

Geometric Figures and Taxicab Geometry….

Many geometric figures are defined in terms of distances: Circles, Ellipses, Hyperbolas, and Parabolas, for example. How will these figures appear in Taxicab Geometry?

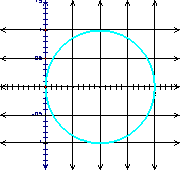
Let’s first look at the Circle. The circle is defined as the set of all points in a plane at a fixed distance from a fixed point in the plane. The fixed point is called the center of the circle, and the fixed distance is called the radius of the circle. Here is our circle with radius of 2:

Now, how about in Taxicab Geometry? The circle is still defined with a radius being a fixed distance from a point being the center, but it takes on a different look…. Let’s see:

The circle looks like what we know as a square! What about other figures? What will they look like?

How about a Hyperbola? Let’s say John and Bob want to meet on the weekend, however, Bob must walk 3 blocks less than John (he has a broken leg). Where area all possible places they might meet?

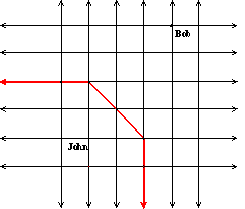
You get one leg of a Hyperbola. All points on the red line meet the desired requirements. To put it in terms of a formula, you get |F₂ to Point| - |F₁ to Point| = 3. What if we turn it around, and Bob has the broken leg. Utilizing the formula |F₁ to Point| - |F₂ to Point| = 3.

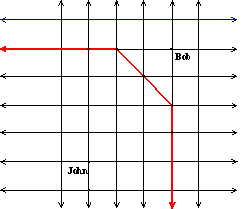
What about an Ellipse? Let’s say John and Bob want to meet, but they only want to walk a combined distance of 9 blocks. Where are all locations where they might meet? If you plot all the possible points, connect the lines around these, you get an Ellipse. The formula for an ellipse looks like: |F₁P| + |F₂P| = a constant, or in this case < 9.

Return to 6690 Page