Day 1 – Circles
In this Instructional Unit on
Circles, we’ll examine various definitions involved with circles, many of the
theorems associated with properties of circles and their proofs, and other
material relating to circles. To begin,
let’s take a look at basic properties and definitions of circles.
A circle, by
definition, is the set of all
points in a plane that are equidistant
from a given point, called the center of the circle.
There are three kinds of
segments related to circles.
1.
The radius
is a segment whose endpoints are
the center of the circle and a point on the circle.
2.
A chord is
a segment whose endpoints are points on the circle. When the chord goes through the center, the
chord will be the diameter.
3.
The diameter
is the distance across the circle through the center.
A diameter is a chord that
contains the center. The diameter is
twice the radius.
We also discuss specific
lines that involve circles:
A secant is a line
that intersects a circle in two points.
A tangent is a line in
the plane of a circle that intersects the circle in exactly one point.
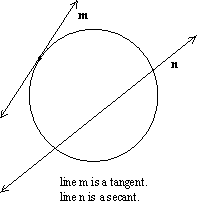Let’s take a look at what these look like:
Because all circles have the
same shape, all circles are similar.
However, two circles are congruent if and only if their radii are
congruent. Two circles are concentric
if they meet the following requirements:
1.
They lie in the
same plane.
2.
They have the
same center.
3.
They have radii
of different lengths.
In a plane, two circles can
intersect in two points, one point, or no points. Coplanar circles that intersect in one point
are called tangent circles.
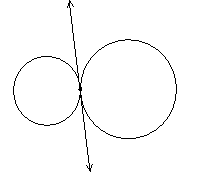
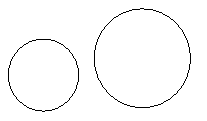
Let’s examine this…
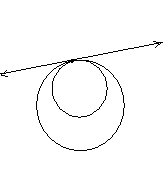
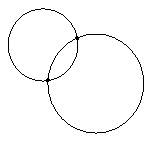
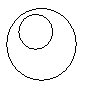
2 points of intersection No points of intersection Tangent
Circles
A line or segment that is
tangent to two coplanar circles is called a common tangent. There are two types of common tangents: a common internal tangent or common external
tangent.
A common internal tangent
intersects the segment that joins the centers of the two circles. A common external tangent does not
intersect the segment that joins the centers of the two circles. How can we tell whether we are dealing with a
common internal tangent, or common external tangent? Let’s examine…
In a plane, the interior of a
circle consists of the points that are inside the circle. The exterior of a circle consists of the
points that are outside the circle.
Properties of Tangents
The point at which a tangent
line intersects the circle to which it is tangent is the point of tangency. Following are a few theorems involving points
of tangency, and the proofs of each of these theorems.
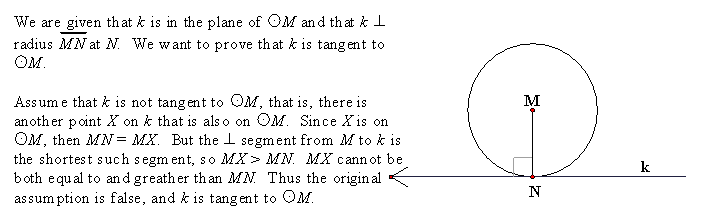
1ST Theorem: If a
line is tangent to a circle, then it is perpendicular to the radius drawn to
the point of tangency.
Proof of 1ST Theorem:
2ND Theorem: In a plane, if a line is perpendicular to a
radius of a circle at its endpoint on the circle, then the line is tangent to
the circle.
Proof
of 2ND Theorem:
ACTIVITY: Examining the relationship between two tangents that
are drawn from a point outside a circle.
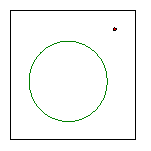Materials:
Compass, Patty Paper, Straightedge
Step 1: Use a compass to draw a circle on patty
paper.
Step 2: Draw a point outside the circle.
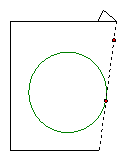Step 3:
Carefully fold the paper so that a tangent is formed from the point to
one side of the circle. Use a
straightedge to draw the segment. Mark
your point of tangency.
Step 4: Repeat Step 3 for a tangent line that
intersect the tangent line in Step 3.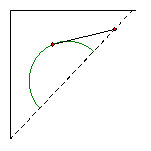 
Try these:
1.
Fold the paper so
that one tangent covers the other.
Compare their lengths. What do
you see?
2.
Make a conjecture
about the relationship between two tangents drawn from a point outside a
circle.
3RD Theorem: If
two segments from the same exterior point are tangent to a circle, then they
are congruent.
Proof of 3RD Theorem:
