
Assignment
#1
Graphing
By
Michelle
Nichols
Look
at the following graphs of the form: xn + yn = 1
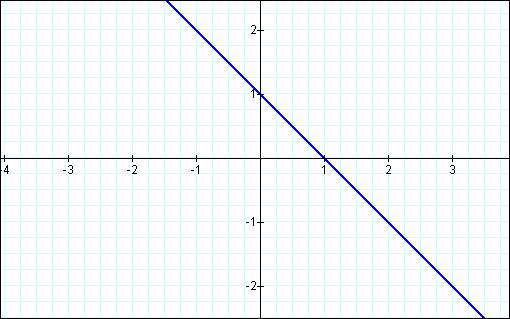
x +
y = 1
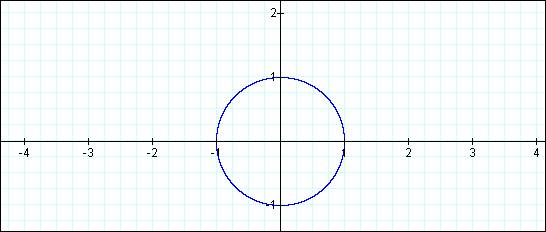
x2
+ y2 = 1
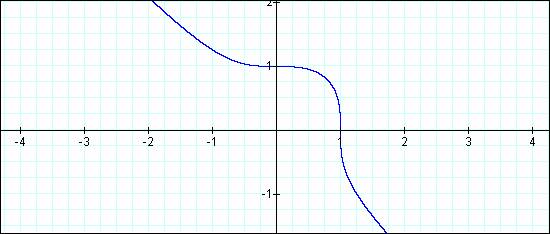
x3
+ y3 = 1
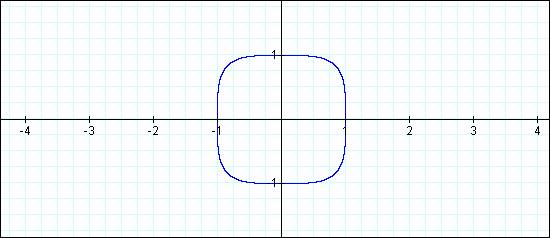
x4
+ y4 = 1
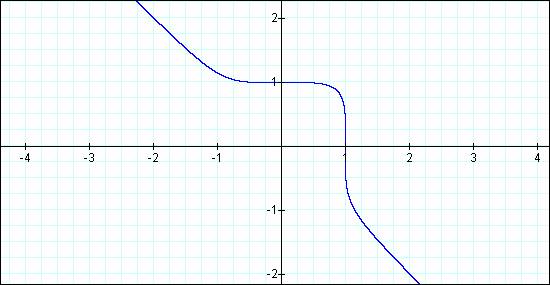
x5
+ y5 = 1
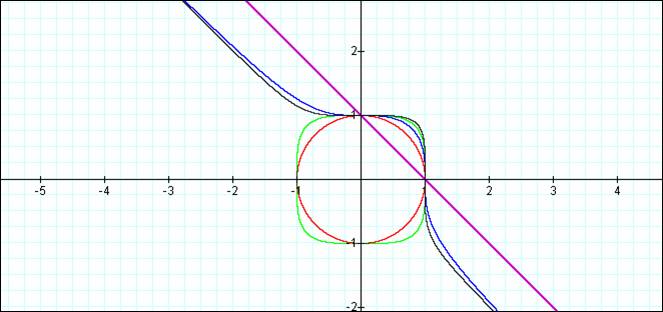
Notice the following about each of the graphs:
· The exponent “n”
determines whether our graph will be continuous or closed.
· “n” as an even
number produces a closed graph.
· “n” as an odd
number produces a continuous graph.
· As “n” increase,
the form, whether closed or continuous, forms a square-like shape around the
origin.
Look at the equations together on one graph.
What do you think the graph will look like for the equation x24
+ y24 = 1?
Given the data collected from the previous graphs, one can assume
the graph will be closed, and near the shape of a square. Let’s see…
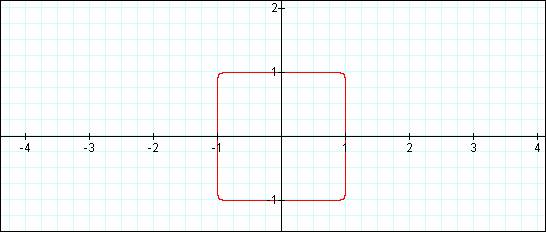
x24
+ y24 = 1
The assumption was correct!
Now how about x25 + y25 = 1? For this graph, if the path follows as before
with odd “n” characters, it should be a continuous graph, curved much like a
square around the origin. Let’s see…
x25
+ y25 = 1
Correct again!
So given the previous graphs, the equation xn + yn
= 1, follows the form of a line for odd “n”, with a square-like shape around
the origin, and for even “n”, a closed square-like shape around the
origin. To see this graph animated in
Graphing Calculator, follow this link: animation