
Assignment #10
Parametric Equations
By
A
parametric curve in the plane is a pair of functions:
x = f(t)
y = g(t)
where the two continuous functions
define ordered pairs (x,y). The two
equations are usually called the parametric equations of a curve. The extent of the curve will depend on the
range of t and your work with parametric equations should pay close attention to
the range of t. In
many applications, we think of x and y “varying with time t” or the angle of
rotation that some line makes from an initial location.
A
cycloid is the locus of a point on a circle that rolls along a line. Let’s look at the parametric equations for
the cycloid and graph it.
Parametric
Equation for the Cycloid:
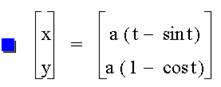
And
it’s graph…
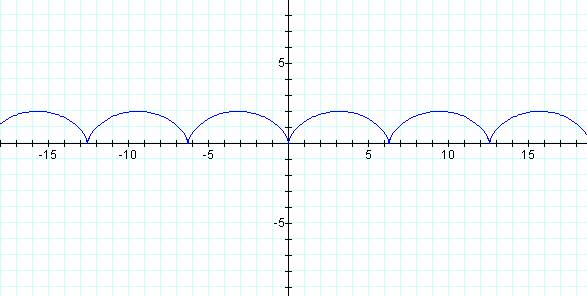
Now
let’s look at the GSP sketch.
·
Start off by constructing a line and a point on
our line.
![]()
·
Next, we’ll construct a line through the point and
perpendicular to the original line. Then
construct a circle (NOTE: this will be the size of our rolling circle), using
our point on the line as the center.
Choose your point on the circle and the center, and construct a segment
(this will be used below to create our rolling circle).
·
Next step:
Select the point on the circle, and the original line, and construct the
line parallel.
·
Place a point on the parallel line just
created. Choose the segment created
above in the circle and our point just created to construct a second
circle. Construct a segment from center
to point on circle to be the spoke on the wheel.
·
All of the construction lines can now be
hidden. We have no need for them. Next, we’ll animate our sketch. Choose the center of the circle and the point
on the circle. Go to “Edit” and “Action
Buttons” and “Animation”. We also need
to trace the outer point on the circle.
(Highlight the point, “display”, “trace point”) Click on our Animate
button, and we have our cycloid.

Click
here to see an animation of this
sketch. Note: You must have GSP.