
Assignment 11
Parametric
Equations
By
Michelle Nichols
When
looking at an equation of the form 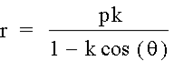 , or
an equation similar to this, the graph will take the shape of some conic,
depending on the value of k. “k”
represents the eccentricity of the conic.
What effect will changing k have on the graph? Examine changing k…
, or
an equation similar to this, the graph will take the shape of some conic,
depending on the value of k. “k”
represents the eccentricity of the conic.
What effect will changing k have on the graph? Examine changing k…
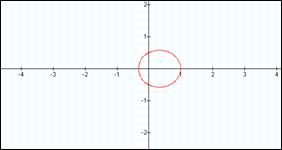
k < 1 k
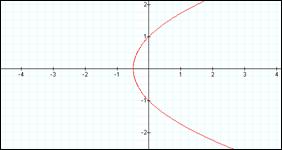
= 1 k
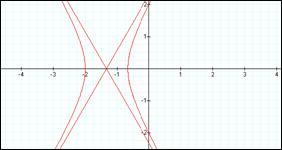
> 1

·
k < 1 creates an ellipse.
·
k = 1 creates a parabola.
·
K > 1 creates a hyperbola.
Look
closer at k < 1, and changing p…

A
negative p puts the ellipse’s center on the negative side of the axis, a
positive on the positive axis. Smaller p
makes a smaller ellipse, larger p larger ellipse.
What
about when k = 1, changing p?

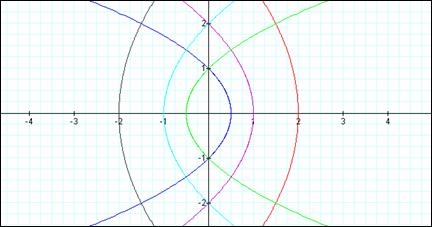
The
p causes the direction of the parabola.
When p is negative, the parabola opens to the left. If p is positive,
the parabola opens to the right. Also,
the size of p determines the width of the parabola. Smaller p, skinnier parabola, and
vice-versa.

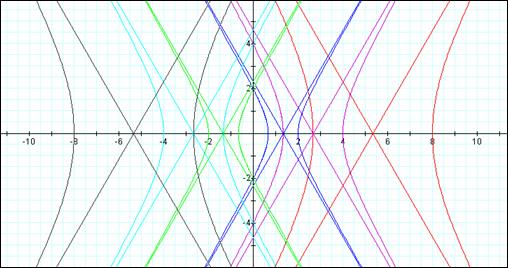
Changing
p on the hyperbola graph has the same effect as on the others. “p” determines the width of the hyperbola and
the location on the x-axis.
Now
what if we look at variations of this equation?
Look first at the following equation:
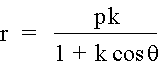
Look
at k = 1, the parabola, with this equation.
How does the graph change from our previous equation?

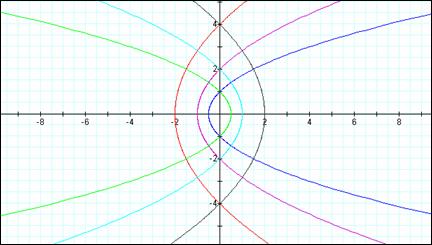
When
the equation is changed to 1 + kcosθ, the parabolas look the same,
however, their direction is changed.
Notice where the parabolas that opened to the left before, now open to
the right. We can assume this property
holds true regardless of k changing.
Look at the animation, and change k, to observe this. Click
Here
What
about another change in the equation – changing cos to sin? Let’s see…
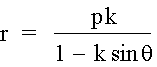 - Look
at the animation of this equation in GSP – click here
- Look
at the animation of this equation in GSP – click here
Now,
observe the above equation with the same changing values of p, and k >
1. What happens?

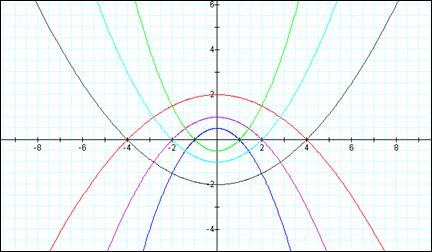
Changing
from cos to sin in the equation moves the parabola to an up/down
direction. Observing other values for k
shows brings the same solution. Look at
the graphs of the ellipse to see.

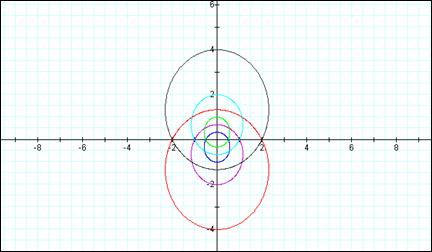
Finally
we’ll observe changing to a (1 + ksinθ).
What effects does this have? Will
they be the same as when we looked the cos value? Let’s see…

Yes! As before, changing the plus sign or minus
sign at the bottom creates the opposite effect on the ellipse.