
Assignment #3
Quadratic Equations
By
Michelle
Nichols
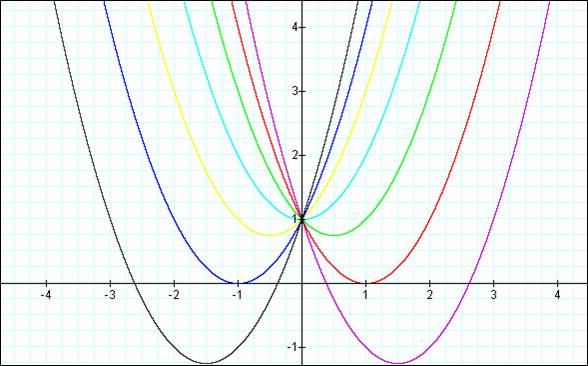
We can discuss the "movement" of a parabola as
b is changed.
The parabola always passes through the same point on the
y-axis ( the point (0,1) with this equation).
·
For b < -2 the parabola will intersect the
x-axis in two points with positive x values (i.e. the original equation will
have two real roots, both positive).
·
For b = -2, the parabola is tangent to the x-axis
and so the original equation has one real and positive root at the point of
tangency.
·
For -2 < b < 2, the parabola does not
intersect the x-axis -- the original equation has no real roots.
·
For b = 2 the parabola is tangent to the x-axis
(one real negative root) and for b > 2, the parabola intersets the x-axis
twice to show two negative real roots for each b.
If we examine the vertices of each of these graphs, here
is what we see…
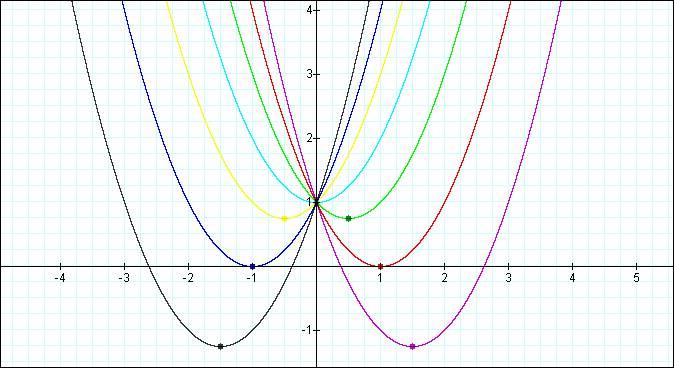
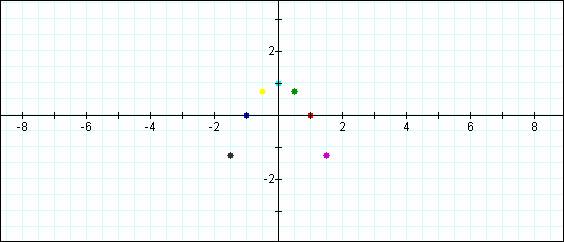
The locus of the vertices seems to form a parabolic
shape. Take a look at the graph of the
points again without the parabolas.
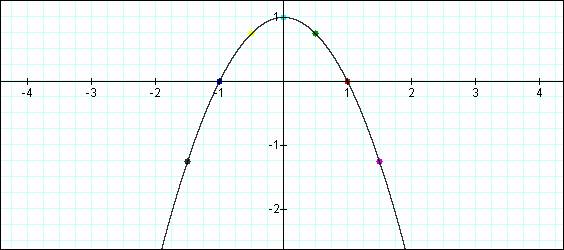
The locus
of the vertices of our parabolas above create a parabola with the vertex at (0,1) and the direction facing downward, thus the equation y =
-x2 + 1.