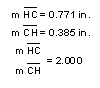Assignment
#4
Centers
of Triangles
By
Michelle
Nichols
Centroid
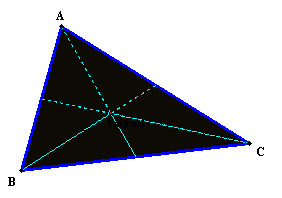
The Centroid of a triangle is the intersection
of the medians, or the center of gravity.†
It is formed by finding the midpoints of the triangle, connecting each
midpoint to the vertices, and connecting their intersections.
Incenter
The 3 angle bisectors of a triangle intersect at a point called
the Incenter of a triangle.† It is the center of the largest circle that
will fit inside the triangle.† Look at
the Incenter:
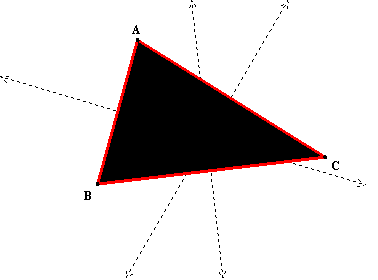
Circumcenter
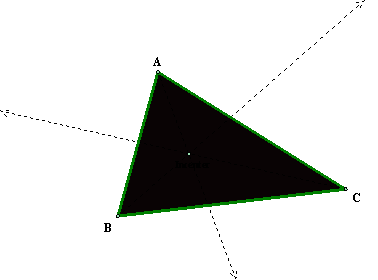
The circumcenter is the intersection of
all 3 perpendicular bisectors of the sides of a triangle.† Itís called the circumcenter
because it is the center of a circle that passes through all of the vertices of
the triangle.†
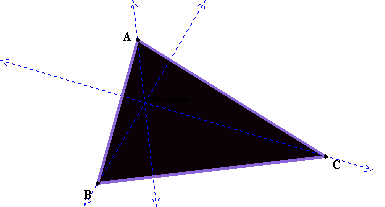
Orthocenter
The Orthocenter is the intersection of the 3 altitudes of a
triangle.† An altitude of a triangle is a
segment that is drawn so that is passes through the vertex and is perpendicular
to the opposite side.†
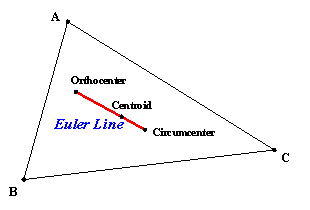
Euler Line
The centroid, circumcenter,
and orthocenter of a triangle are all collinear.† The Euler Line is the line that connects all
of these points.†
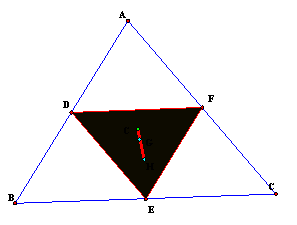
Exploration
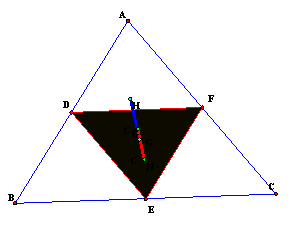
Take any triangle.† Construct
a triangle connecting the 3 midpoints of the sides.† This is called the MEDIAL triangle.† It is similar to the original triangle and ľ of
its area.† Construct G, H, C, and I for
this new triangle. †Compare to G, H, C,
and I in the original triangle.†

Now if we construct the Euler Line for both, thus observing G, H,
and C, letís see how they compare.†
Large Triangle†††† ††††††††††††††††††††††††††††††††††††† †††††††††††††††††† Medial Triangle
 †††††††††††††††††††††††††† †††††††††
†††††††††††††††††††††††††† †††††††††  ††††††††††††††††
††††††††††††††††
The points lie on the same line, however, the locations and distances
between each change.† The larger
trianglesí Euler Line appears to be twice the distance.† When measurements and ratios are taken, we
find this to be exactly true.† The Larger
triangle Euler Line has a 2:1 ratio to the medial trianglesí Euler line.† Also, the centroid
and orthocenter swap sides.†
Observe the
triangles together:†††††††††††††††††††††††