
Assignment 6
Parabolas – GSP
By
Michelle Nichols
A
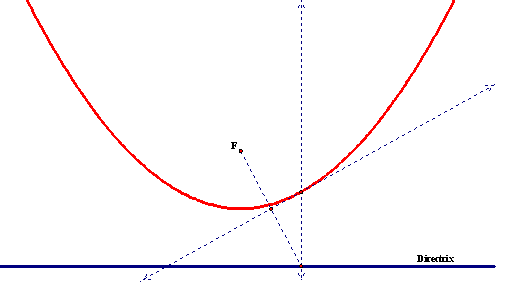
parabola is the set of all points equidistant from a line, called the directrix, and a fixed point, called the focus.
Let’s
consider the construction of a parabola in GSP, starting with a line and point
not on the line…
1. Construct a line (the directrix).
2. Construct a point somewhere
above or below the line. Label this
point F (focus).
3. Connect the point and the
line with a segment.
4. Construct the midpoint of
this line segment, and then construct the perpendicular line through this
point.
5. Select the point on the directrix, and the line, and construct a perpendicular line
through this point.
6. Construct the intersection
of this perpendicular line and the previous perpendicular.
7. Select the point on the line
and then this intersection point, and construct the locus.
8. This final step creates our
Parabola.
We
can also trace our point on the parabola, then move
the point on the Directrix to obtain a similar picture
(the same parabola).
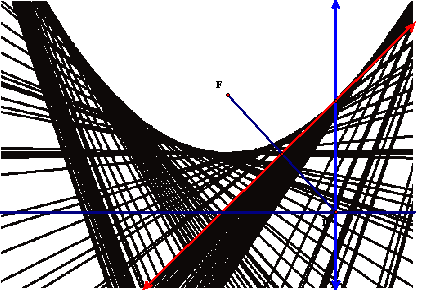
How
do we know this is a Parabola? Using our
construction and the definition of parabolas we know that this not only looks
like a parabola, it is! Within this
construction are triangles that will help with the proof. If we name each of our points, we can connect
segments and prove the construction. See
the adjusted construction:
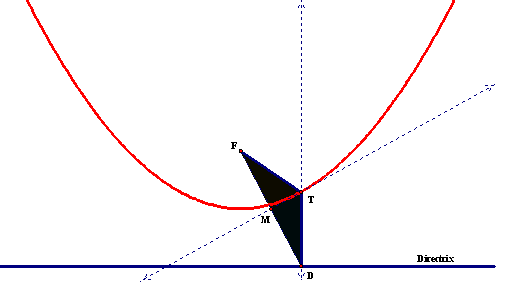
And
the Proof:
·
By construction, |FM| ≈ |DM|.
Point M is the midpoint between F and D.
·
Angle DMT ≈ Angle FMT. A
perpendicular was constructed through M to create these 2 angles, therefore
making both of them right angles.
- |MT| ≈ |MT|, by the Reflexive
Property of Congruence, which says any figure is
congruent to itself.
- So, ▲FMT ≈
▲DMT, by
SAS.
- We now know that |FT| ≈
|DT|, by CPCTC.
- So our construction works – The distance from the Focus to the Point on the Parabola is equal to the distance from the Directrix to the point on the Parabola.