
Assignment
#7
TANGENT
CIRCLES
By
Michelle
Nichols
Given
two circles and a point on one of the circles, construct a circle tangent to
the two circles with one point of tangency being the designated point.
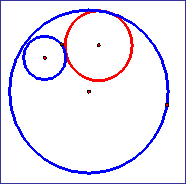
When the center point of our
tangent circle is traced, what do we get?
Let’s see…
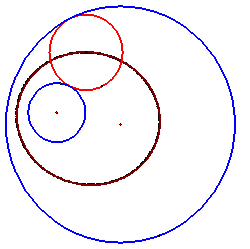
We get an ellipse, with Foci
at center of both our original circles.
What if the circles are disjoint, meaning the smaller circle lies
outside the larger circle? Observe this
construction…
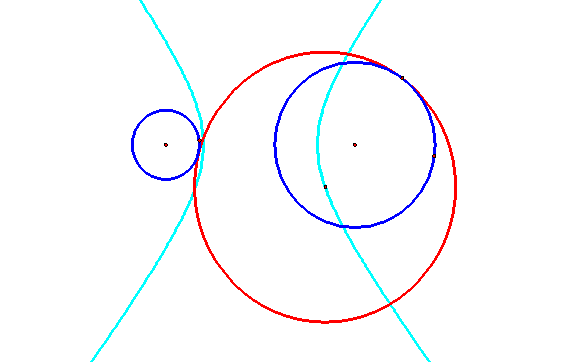
The locus when the circles
are disjoint is a hyperbola, rather than an ellipse. The Foci, once again, lie at the radius of
the small circle and large circle. Take a look at the sketch of the locus of
the hyperbola and ellipse, once again, without the circles.


For a GSP script tool of the
tangent circle, click here.