
Assignment #9
Pedal
Triangles
By
Michelle Nichols
Let triangle ABC be any triangle. Then if P is any point in the plane, then
the triangle formed by constructing perpendiculars to the sides of ABC (extended
if necessary) locate three points R, S, and T that are the intersections.
Triangle RST is the Pedal Triangle for
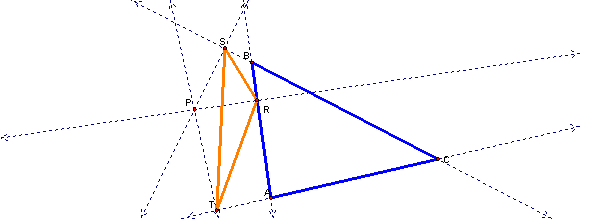
To construct the Pedal
Triangle, draw triangle ABC and point P is any point in the plane (See picture
above). Then construct the perpendiculars to sides AB, AC, and BC from the
point P. The intersections of the perpendiculars and the sides are points R, S,
T. Our Pedal
Triangle is the orange triangle, RST.
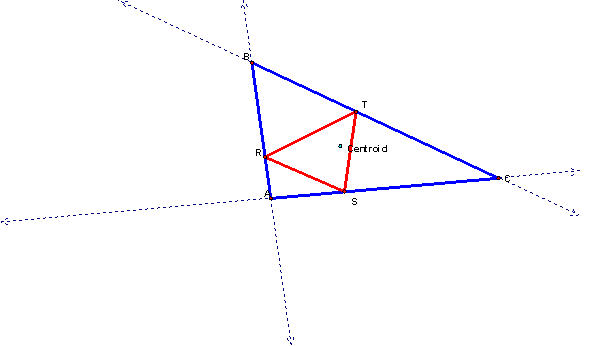
What
if the Pedal Point P is the centroid of the triangle?
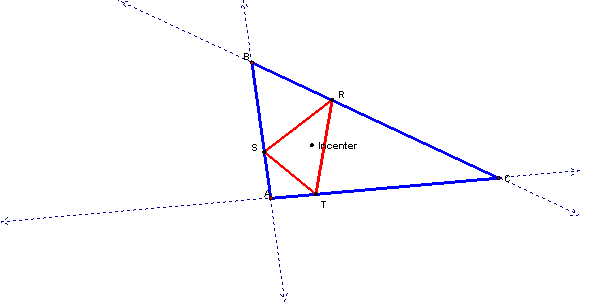
What
if P in the incenter?
What
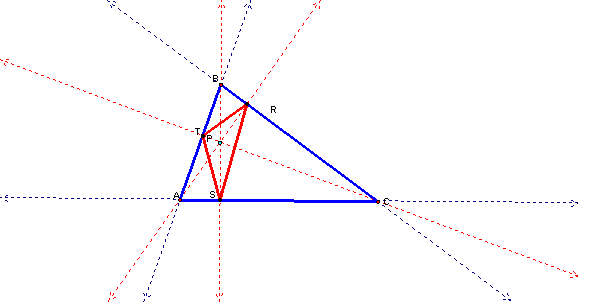
if P is the Orthocenter? Even if outside of ABC?
Orthocenter Inside the
Triangle
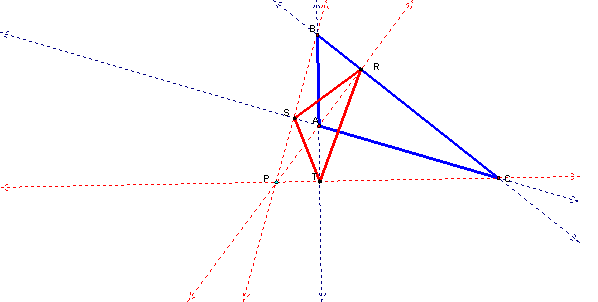
Orthocenter Outside the
Triangle
What
if . . . P is the Circumcenter . . . ? Even if outside ABC?
Circumcenter
Inside the Triangle
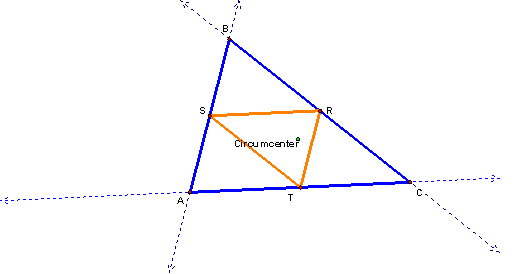
Pedal Triangle RST lies inside ▲ABC
when point P is the circumcenter.
Circumcenter
Outside the Triangle
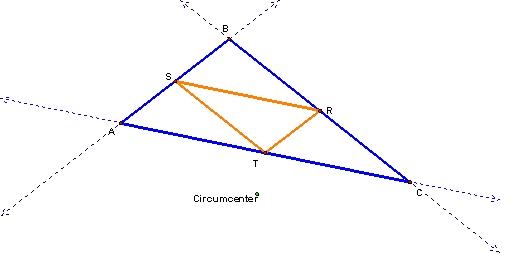
If the Circumcenter
is outside the Triangle, the Pedal Triangle is still inside ▲ABC
What
if . . . P is the Center of the nine point circle for triangle ABC?
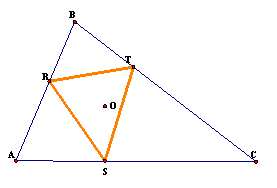
What
if P is on a side of the triangle?
If P is on a side of the triangle, then the
point P is shared with one of the vertices of ▲RST.
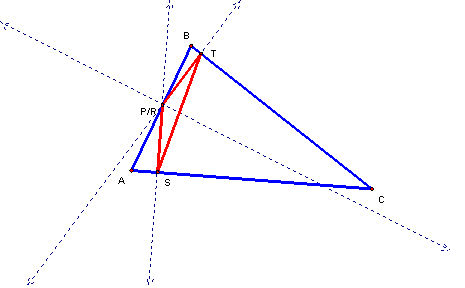
What if P is one of the
vertices of the triangle?
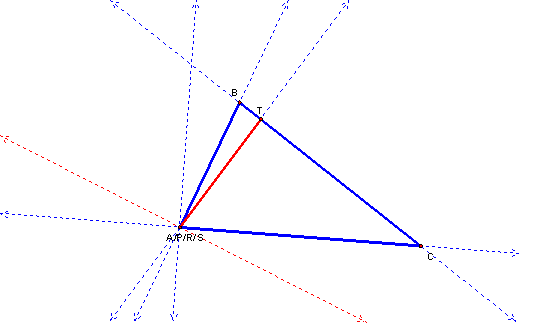
When P is one of the vertices
of the triangle, a straight line is formed.
In the above sketch, A,P,R,S all share the same
point.
Find
all conditions in which the three vertices of the Pedal triangle are colinear (that is, it is a degenerate triangle). This line
segment is called the Simson
Line.

When P lies on the circumcircle
of ▲ABC, the Simson Line is formed.