
EMAT6680 Assignment 10
The Cycloid
By Kevin Perry
Parametric
Equations
In this discussion we will explore parametric equations as useful tools and specifically investigate a type of equation called a cycloid.
Definition
A set of parametric equations is two or more equations based upon a single variable or variables (but not each other).† Functions of the form y = f(x) can be broken down into a set of parametric equations y = f(t) and x = f(t).† This is often the method employed by computer aided graphing programs to display graphs of functions.† The other variable can be thought of as time or angle, but is simply just a parameter that the equations are based upon.
Simple Parametric
Equations
To get the feel of parametric equations, we can first explore a simple example.† Letís first look at
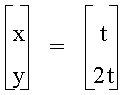
What this equation is saying (in vector form) is that x is equal to t and y is equal to twice t.† Therefore, if t is any real number, we have a set of x and y that can be plotted and represent all of the pairs of x and y that satisfy the parametric equation.†† The resulting graph looks like
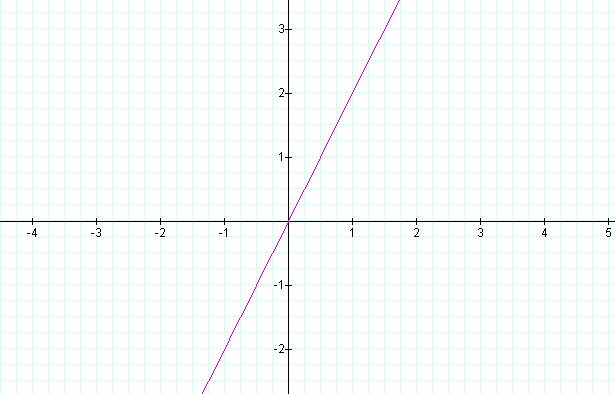
Of course this is a simple example, and it is easy to show that y = 2x, and we are not surprised that the graph is a straight line.
Another simple parametric equation is
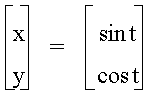
which has a graph that looks like
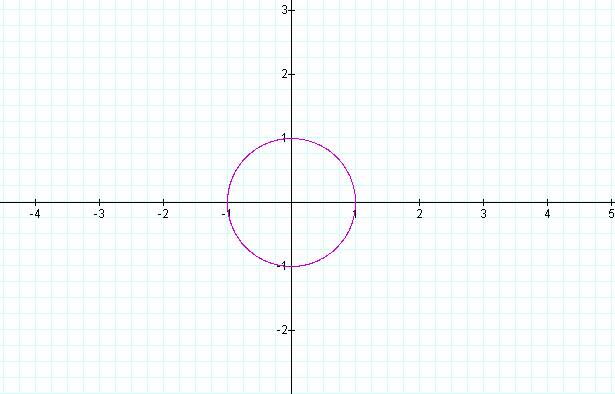
In this case, if we think of t as the angle about the origin, the point (x,y) on the circle is the cosine of the angle and the sine of the angle.† And the graph above is the unit circle.
Using Parametric
Equations to Describe Complex Movements
Using parametric equations can be very useful for describing complex situations. An example would be to write equations for the movement of objects over time.† The movement of the object in any particular direction may be independent of all other factors except time, and therefore an equation describing that portion of the movement will only include the variable time.
We want to use parametric equation to describe a complex movement.† For our moving point, we pick a single point on the edge of a bicycle tire as is rolls straight down the street.† A visual model of this looks like

As the tire rolls down the street, the point P on the tire will move closer to and farther away from the street, but it will also move down the street just as the tire does.† We need to describe this motion with some equations.
The thing about parametric equations is that there are independent of each other, and in the case of describing motion, this independence can help us in writing the equations.† Letís first look at the vertical movement without thinking about the horizontal movement.† If the tire was simply rotating, the point P would be tracing out the shape of a circle.† If we think of t as the angle that P makes to the center of the circle (in radians) and we remember that the simple parametric equation that we used above traced out the unit circle.† We can conclude that the distance y from the street is going to somehow relate to the sine of t.
If we pick a moment in time where P is on the street and say that that is equal to t = 0 we can set that point as the starting point for the equation.† Our angle from the center of the circle in this case is -90 degrees (or Ėπ/2), therefore when t = 0 we want the sine of Ėπ/2.† Therefore our equation for y (the distance form the street) is
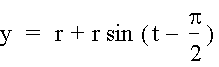
where r is the radius of the tire.
Now we must decide whether the tire is moving toward the right or the left.† If we choose the tire to roll to the right, we can see that the point P will move clockwise around the circle, and therefore the angle from the origin will get more and more negative.† We can therefore modify our equation for y to be
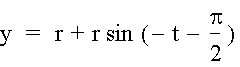
This equation will represent the distance from the street as the bicycle tire rolls down the street.
Next, we want to tackle where the point P will be in the x direction as the bicycle tire rolls along.† The equation for y should be some clue, as we can first think only about the tire rotating.† From the unit circle above, we know that the x position is related to the cosine of the angle from the center (in radians), and from our equation for y, we know the angle of point P from the center, therefore part of x can be represented as
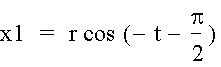
Next, we must determine the portion of x as the tire rolls down the street.† We know that the arc of the tire as it rolls an angle of t radians has a length of rt, therefore we know that the center of the tire moves a distance of rt as the tire rotates t radians.† So, adding that factor into the formula for x, we get
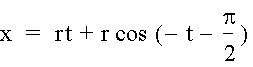
Therefore, our parametric equations for the movement of a point P on the edge of a bicycle tire as it rolls straight down the street are
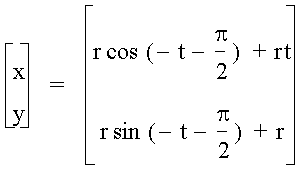
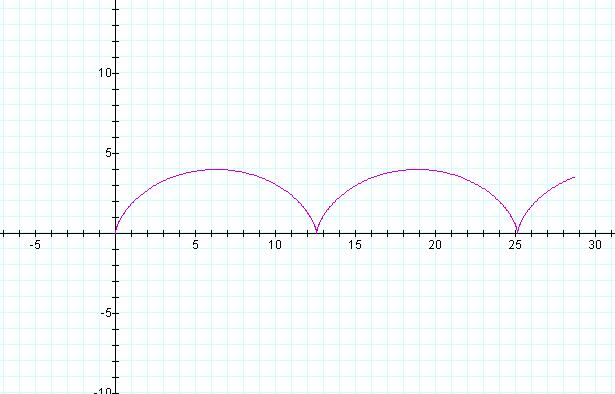
And the graph of these equations as t goes from 0 to 15 and for a tire radius of 2 ft. is
If you would like to see a GSP demonstration of the movement traced out, click here.
This function is called a cycloid.
Conclusions and
Extensions
If instead of picking a point on the edge of the tire, what if we picked a point on the spoke of the wheel?† Then what would the equations of the motion of the point look like?
The quickest way to think about this change is to remember that the x and y directions both depend on the circle traced as the tire rotates.† Now that the point of interest is not on the edge of the tire, the radius of the circle of movement is now smaller.† If we say the point is now a distance d from the edge of the tire, the parametric equations now become
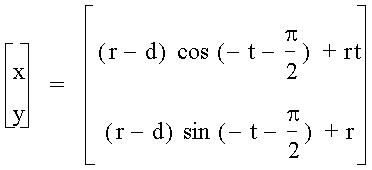
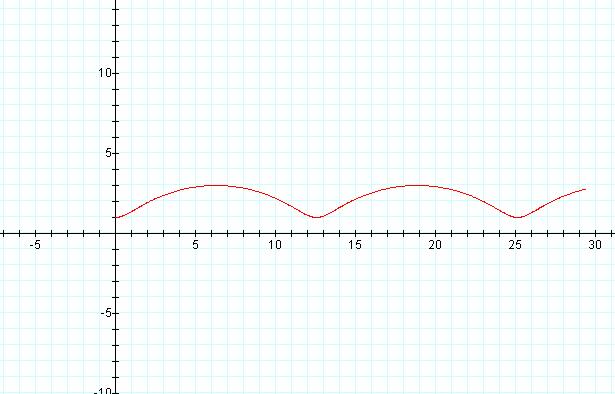
And the graph now looks like (with r = 2 and d = 1)
Further extensions would be to investigate what the equations would looks like for other types of motion. For example, how would you describe the motion of a tether-ball as it rotates around a pole?
We have seen in this investigation that parametric equations can be useful for describing complex situations by breaking down the problem into independent equations based on the same variable.† We have seen that parametric equations are powerful, but we have only scratched the surface of their utility as an analysis tool.