
EMAT6680 Assignment 6
Geometerís SketchPad Football Problem
By Kevin Perry
The Football Field
Goal Problem
In this assignment we will solve a problem using Geometerís SketchPad as a solution tool.† The problem we will investigate is that of the football field goal.
The football rules in college football were changed a few years ago to make the field goal uprights 5 feet narrower than they were previously. Many game commentators have harped about how much harder it is to kick field goals from the hash marks. Assume the field goal is attempted from the hash marks. At what yard marker does the kicker have maximum angle to the two uprights?† Is there any merit to some commentatorís argument to take a penalty in order to have a "better angle" on the field goal kick?
Background
Information
The diagram below is from the NCAA website, and defines the dimensions of the football field.† We can see from the diagram that the field is 160 feet wide, the hash marks are centered and are 40 feet apart, and that the field goal is centered and the uprights are 18.5 feet apart.
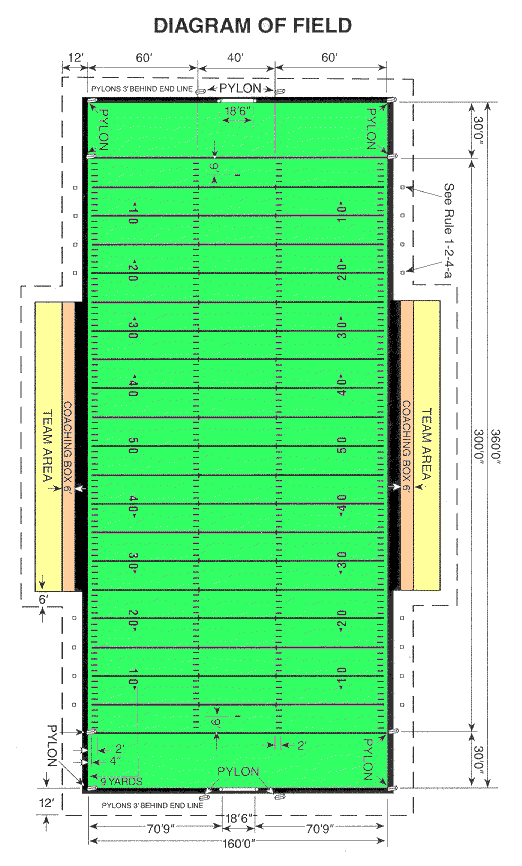
The endzone is 10 yards long (30 feet), and the standard unit of measurement in football is the yard.
A field goal is kicked from anywhere between the hash marks, and it must go between the uprights for it to be counted.
The Football Field
Model
To start our discussion of the problem, we must first model the field in GSP so that we can make measurements and construct supporting evidence.† The model of the football field can be found in this GSP file.† A snapshot of one end of the field looks like this
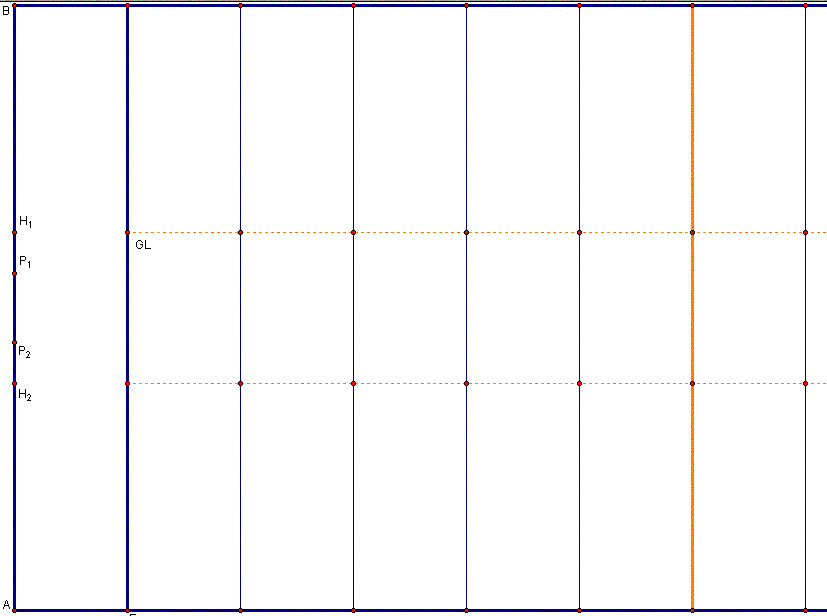
For the stated problem, we need to set up the field goal along one of the hash marks.† The field goal kicker has to kick the ball in the angle defined by his kicking point and the two goal posts.† In GSP this looks like
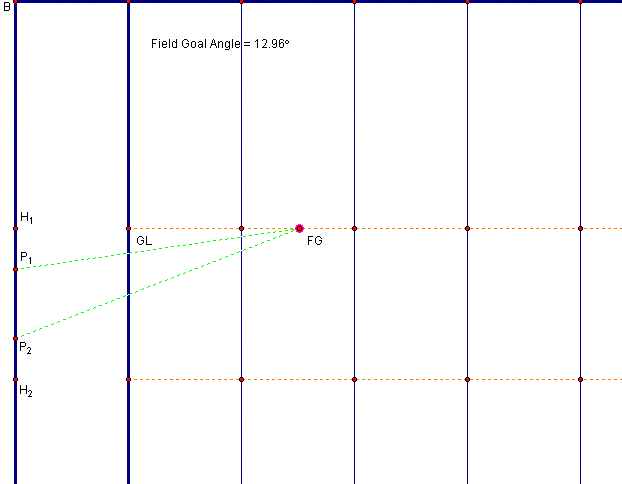
In the above situation, the field goal kicker is approximately kicking from the 15 yard line, and his field goal angle is 12.96 degrees.
The first part of the question is what yard line will give the kicker the maximum angle to the field goal.† With some investigation on GSP, we can get the angle from different distances.
|
Yard Line (yards) |
Field Goal Angle (degrees) |
|
0 |
24.29 |
|
10 |
15.62 |
|
20 |
11.08 |
|
30 |
8.48 |
|
40 |
6.87 |
From the table and from investigating the GSP construction, we see that the field goal angle always gets smaller as the distance from the goal posts increases. †Therefore, the answer to ďAt what yard marker does the kicker have maximum angle to the two uprights?Ē is at the goal line (the zero yard line).
The second question is also quite obvious from the table and GSP construction.† If the announcers suggest that a team that takes a penalty (and moves farther from the goal line) in order to improve the field goal angle, they are suggesting incorrectly, and should be ignored at all costs!
Another Study
Another common announcer suggestion (and oftentimes a major coaching decision) is to center the ball in the field in order to improve a field goal chance.† To study this theory, we can use the same GSP model.
As shown below, we will take the 20 yard line as our field goal distance.† The figure below shows the field goal angle from one of the hash marks.

But we can also construct the field goal from the center of the field (centered between the hash marks).† The figure below shows the comparison.
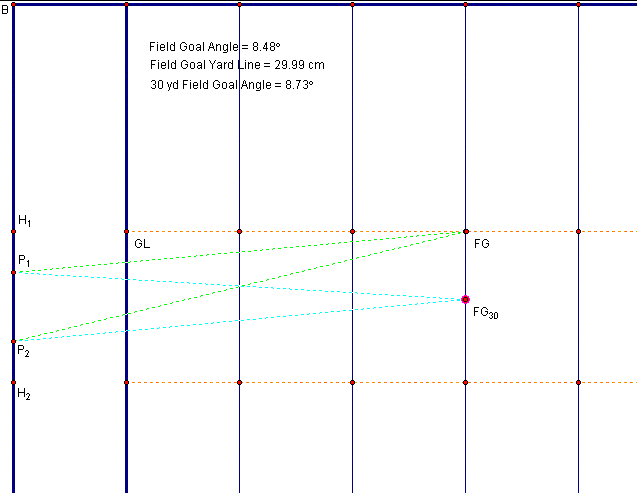
Therefore, we can see that for a field goal at the 30 yard line the difference in that field goal angle is approximately 0.25 degrees.† Again, it seems that the conventional wisdom is at least inaccurate in this case.
Conclusions and
Extensions
This problem showed that GSP can be used to set up a mathematical model for a real life situation.† With the model, one can investigate lots of mathematical problems that may come up real life, and either prove or disprove the common beliefs.† This particular model (the football field) has a rich amount of real life situations that can be investigated.† A simple one would be:† How far does the quarterback have to throw if he is along the sideline and throws back to the opposite hash mark?