
EMAT6680 Assignment 7
Tangents of Circles
By Kevin Perry
Tangents of
Circles
In this assignment we will explore the situation where we have two circles and the tangent lines and circles that can be constructed.
Tangent Lines to
Two Circles
The diagram below shows a basic setup for this discussion. There are two circles of different radii that are separated (i.e. they do not intersect).
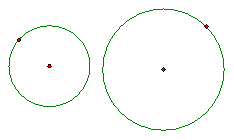
How many different lines are tangent to both circles? There is one that lies on top of both of the circles, one that is the mirror image of the first one on the bottom of both circles. Also, there are two lines that would make an X between the two circles. That is a total of four lines. We will not concern ourselves with the construction of these lines in this discussion. Instead, we will show the four tangent lines and let the reader investigate the constructions. The tangent lines are shown below
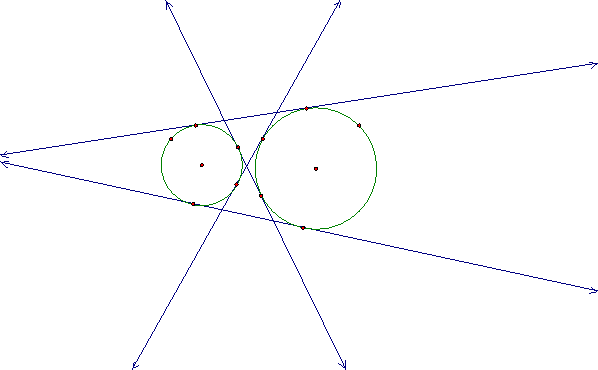
These two sets of tangent lines are special cases of another set of tangents, which we will show later.
We now will switch to two circles that are arranged one inside the other. If we wanted to draw the tangent lines like those above, we would quickly see that they are not possible.

Instead, let’s see if we can construct a circle that is tangent to both of these circles. There are actually two different possible sets of circles that would be tangent to both of these circles. We can use GSP to do an approximate sketch of two new circles.
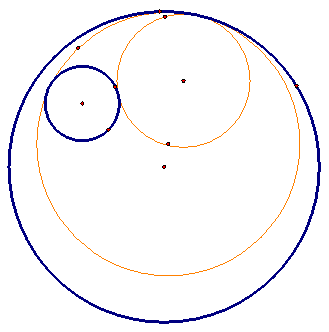
But the interesting thing is that unlike the four tangent lines of two disjoint circles, there are whole sets of circles that satisfy the tangency to both circles. We can again demonstrate this with a sketch

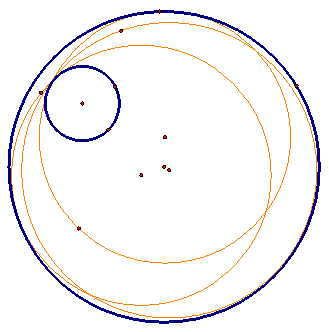
Now that we have seen that there are two sets of circles that are tangent to the two given circles, we can try to construct these circles given the tangent point on one of the circles.
Construction of
the
We first look at the circle that is inside the larger circle but outside of the smaller circle, and it does not enclose the smaller circle.
The first step is to pick the tangent point on the large circle and draw a line through the point and the center of the large circle.
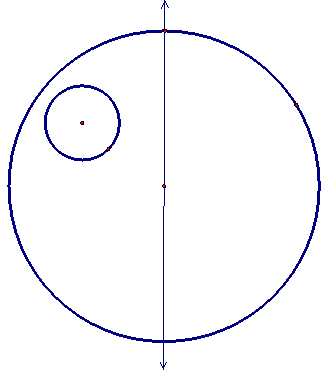
If a circle is tangent to circle A (the larger given circle) at the point P, then the tangent circle must have a center point along this line. We can see this by picking a point on this line and creating a circle through point P.
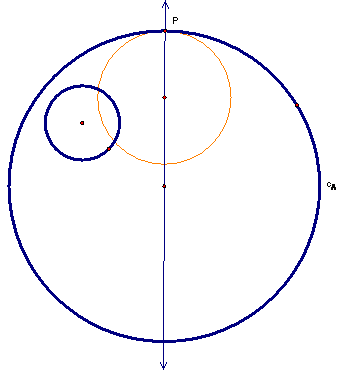
If we knew where the new circle was going to be tangent to circle B (the smaller given circle), we could also say the same thing about center point being on the line between the tangent point Q and the center of circle B. Instead, let’s assume we know where the center of the tangent circle is and construct some key line segments. If we had the center of the tangent circle and constructed a line segment on the line that had the same length as the distance between the two circle centers, we could construct an isosceles triangle as shown below.

But, we don’t know where the point C is. But now we know that there is an isosceles triangle that includes C as a vertex. And we also know that the perpendicular bisector of the base of an isosceles triangle passes through the third vertex. So if we could come up with another way to create the triangle, we could find the location of C. From the figure, we can see that the length of the sides of the triangle are the sum of the radius of circle B and the radius of the tangent circle, and we see that one side of the triangle connects the to center points and more importantly that the other side lies along the constructed line. Therefore, the vertex of the triangle that is outside of circle A is exactly the radius of circle B away from the tangent point P. So if we construct a circle of the same radius as circle B starting a point P, we can get this point.

Therefore, the perpendicular bisector of the line segment between this new point and the center of circle B will pass through the center of the tangent circle. So now we have two different lines that both have to contain the same point. Therefore the intersection of these two lines defines the center point that we are looking for.
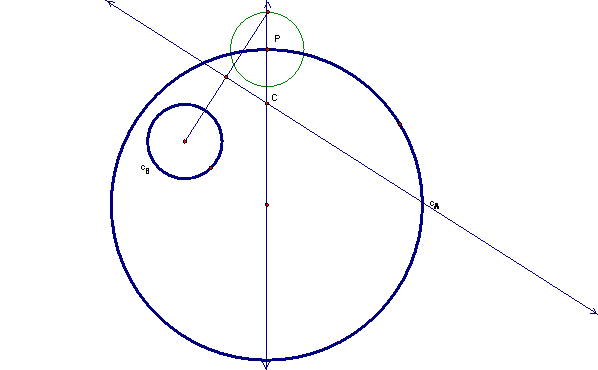
Now we have the center of the tangent circle (point C) and one point that it passes through (point P) so we can construct the tangent circle. We can see that this circle is also tangent to circle B.
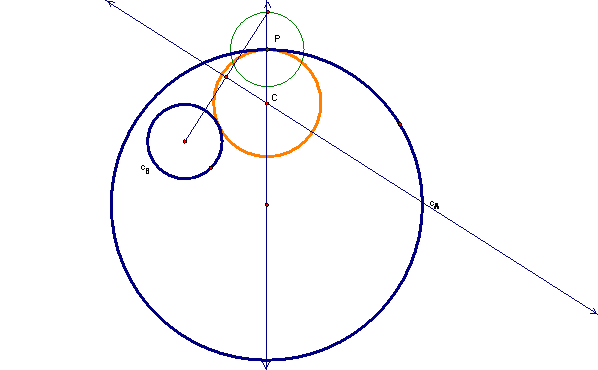
Now, if we hide the construction objects and let P move around the circle, we can see the entire set of circles that are tangent to these two circles in this manner.

Construction of
the
Now we can look at the tangent circle that encloses the circle B.
We know from the first construction that an isosceles triangle will help us locate the unknown center of the tangent circle. And we again remember that the center must lie on the line through the center of circle A and the point P. If we make a quick sketch, we could maybe find a situation that would help us find the isosceles triangle for this case.
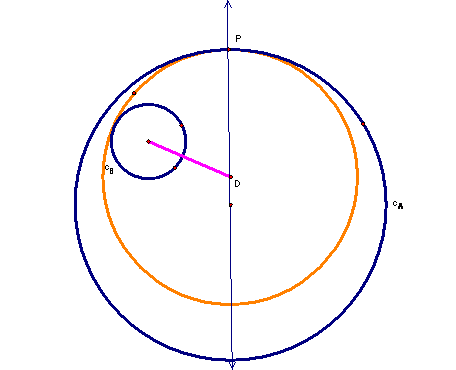
The line segment between the unknown point D and the center of circle B would have a length that is the difference between the radius of the tangent circle and the radius of circle B. So if we again construct a circle about point P that has the same radius as circle B, we can get the point that creates the base of another isosceles triangle.
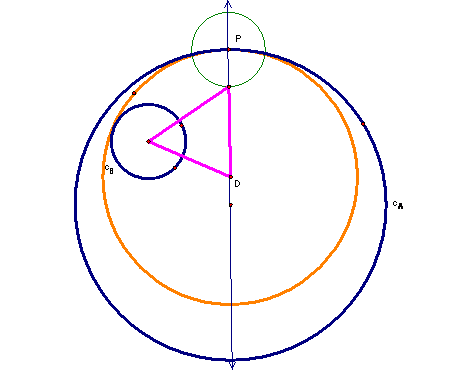
So now the perpendicular bisector of the line segment between the center of circle B and the constructed point will define the line that the center of the tangent point must lie on. Again, the intersection of the two constructed lines defines the center of the tangent circle.

And again, with the center point and one point of the circle (point P), we can draw the tangent circle that encloses circle B.
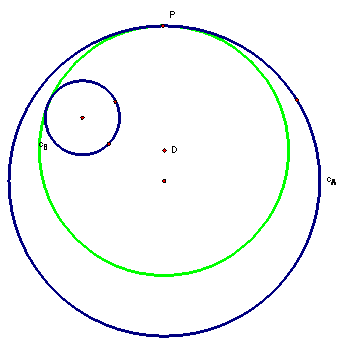
Now as point P moves around circle A, the second set of tangent circles can be seen.

Properties of the
Tangent Circles
We have merely constructed the two tangent circles at a point, now we can change the two given circles and see how the tangent circles change. We start with the situation that we constructed the tangent circles. One given circle is smaller and inside a larger second given circle.

First, we can see that as the smaller circle gets closer to being itself tangent to the larger circle, the green tangent circle approaches the larger circle. Then as the inside circle crosses over and intersects the larger circle, the green tangent circle goes outside the larger given circle and continues to go larger and larger.
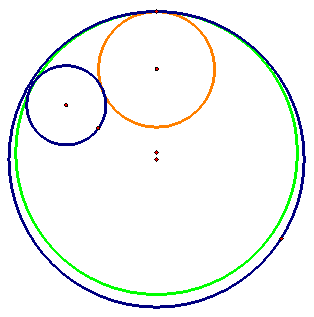

If we examine the subset of the tangent circles when the given circles intersect, we can see an interesting property at a particular point P.
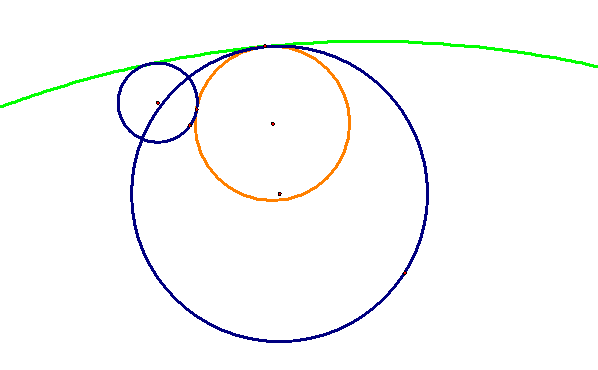
We see that the green tangent circle changes from enclosing the two given to not enclosing either circle. The point at which this transitions between these two properties, the tangent “circle” is a straight line that is tangent to both circles. We recognize this as one of the four tangent lines between two circles. This tangent line will be a part of this set of tangent “circles” as long the smaller circle is not completely inside the larger circle.
If we now pull the smaller circle completely outside the larger circle, we can look closer at a subset of the orange tangent circle.
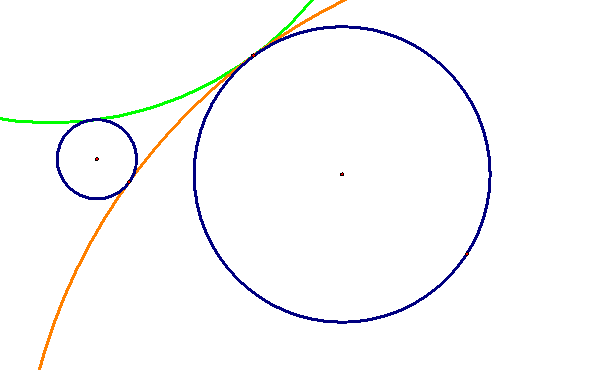
We again see that the subset contains a straight line tangent “circle” that is a tangent line on both of the given circles. This is also on of the four tangent lines that we saw earlier. This tangent line will always be a member of the set of tangent circles as long as the smaller circle is completely outside of the larger circle.
Conclusions and
Extensions
This discussion introduced the concept of tangent circles to two given circles. There are many interesting properties of the sets of tangent circles, and of other points constructed from these circles. For example, the centers of the tangent circles form an ellipse with foci at the centers of the two given circles. A challenging extension to this discussion would be to construct a tangent circle to three given circles.
The reader can explore and experiment with these constructions with a GSP construction.